Situación
Preguntouse aos 100 estudantes dun curso pola súa altura en centímetros, resultando os seguintes datos:
| 173 | 162 | 158 | 180 | 156 | 172 | 170 | 171 | 165 | 164 |
| 154 | 170 | 151 | 167 | 160 | 171 | 172 | 174 | 167 | 177 |
| 159 | 162 | 176 | 169 | 175 | 164 | 180 | 175 | 169 | 158 |
| 181 | 179 | 160 | 181 | 172 | 169 | 151 | 184 | 153 | 163 |
| 177 | 158 | 170 | 170 | 166 | 180 | 172 | 169 | 161 | 157 |
| 156 | 186 | 177 | 164 | 169 | 152 | 165 | 169 | 190 | 174 |
| 166 | 170 | 174 | 160 | 157 | 153 | 183 | 188 | 168 | 155 |
| 156 | 165 | 165 | 159 | 163 | 164 | 166 | 170 | 173 | 155 |
| 165 | 179 | 178 | 168 | 165 | 163 | 175 | 155 | 161 | 172 |
| 179 | 164 | 171 | 169 | 162 | 169 | 174 | 176 | 160 | 181 |
Táboa de frecuencias
- Copia a listaxe de datos e pégaa na Folla de cálculo de GeoGebra.
- Comezamos por definir as clases que se utilizarán. O comando Clases permite indicar ou ben o número de clases ou ben a anchura das clases (e neste caso, tamén onde empezar).
- clases = Clases(A1:J10, 150, 5)
- n = Lonxitude(A1:J10)
- A continuación xa é posible elaborar a táboa de frecuencias cos datos agrupados en clases. Aparecerá na Vista gráfica.
- TáboaFrecuencia(clases, A1:J10)
- Nota: os intervalos resultantes son pechados pola dereita e abertos pola esquerda
Gráficos estatísticos
- Por tratarse dunha variable continua, á hora de representar os datos graficamente queremos optar por un histograma. Para iso é preciso contar cunha lista que conteña a frecuencia absoluta de cada clase.
- frecuencias = Frecuencia(clases, A1:J10)
- Histograma(clases, frecuencias)
- Tamén podemos representar o polígono de frecuencias correspondente.
- polfrec = PolígonoFrecuencia(clases, frecuencias)
Parámetros estatísticos
- Cando se teñen poucos datos é relativamente doado atopar os valores mínimo e máximo, pero cando o tamaño do estudo aumenta precisamos axuda.
- min = Mínimo(A1:J10); max = Máximo(A1:J10) e rango = max - min
- Para obter os parámetros básicos procede igual que na actividade anterior: podes empregar a listaxe enteira de datos.
- media = media(A1:J10)
- varianza = Varianza(A1:J10)
- desvest = sqrt(varianza)
- Neste caso, a diferenza da actividade anterior, non nos imos limitar a calcular a mediana e os cuartís, senón un percentil calquera.
- Para iso, primeiro crea un Esvarador, premendo na icona
 da barra de ferramentas.
da barra de ferramentas.
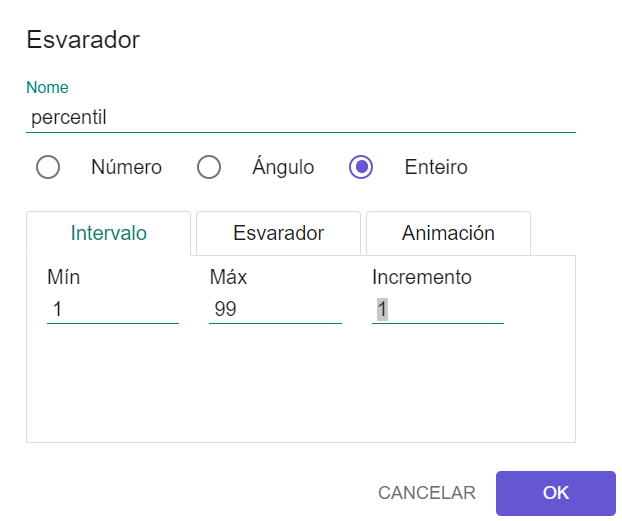
- Isto permitirá que poidamos mover dinamicamente o esvarador e ver como varía o percentil.
- p = Percentil(A1:J10, percentil / 100)
- Para visualizar o significado do percentil, podemos crear un Segmento((clases(1),0),(p,0)) , e dende as propiedades do dito segmento remarcalo cambiándolle a cor e engadindo unha marca no seu extremo dereito.
A ferramenta de análise
- Ao igual que na actividade anterior, GeoGebra ofrece a posibilidade de implementar unha análise dos datos de forma directa.
-
Sitúate na Folla de cálculo e seleccionan co rato -premendo e arrastrando- a listaxe enteira de datos que tes dende o principio.
-
Preme na icona Análise dunha variable
 que atoparás na barra de ferramentas.
que atoparás na barra de ferramentas. -
Na vista que aparece a continuación, podes indicar -na parte superior esquerda- se queres que se amosen os parámetros estatísticos básicos, os datos que se están a usar, e un ou dous gráficos. As mesmas funcionalidades, e análogas posibilidades didácticas, que para o caso discreto.
![]()
-
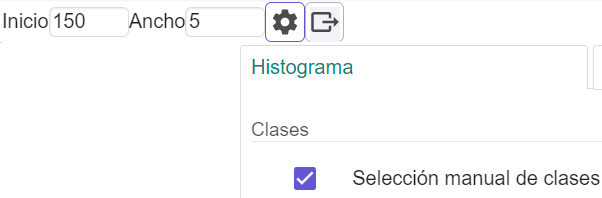
Nesta ocasión interésanos o Histograma. Por defecto permite seleccionar o número de clases mediante un esvarador.
![]()
- Pero, se entras nas súas propiedades
 , poderás marcar a opción de facelo manualmente, e indicar a anchura das clases e o valor no que empezará a primeira desas clases.
, poderás marcar a opción de facelo manualmente, e indicar a anchura das clases e o valor no que empezará a primeira desas clases.