Distribución binomial

• Imos comezar por representar a función de masa de probabilidade dunha distribución discreta como é a distribución binomial \(Bin(n;p)\).
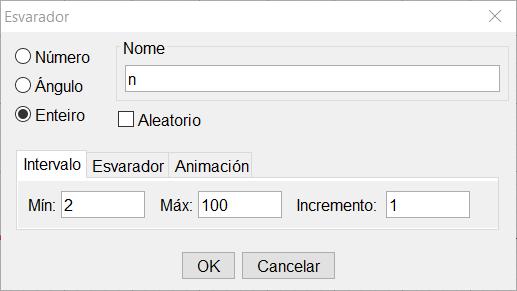
  • Crea un Esvarador para o número de experimentos realizados \(n\), seleccionando a icona correspondente na barra de ferramentas.
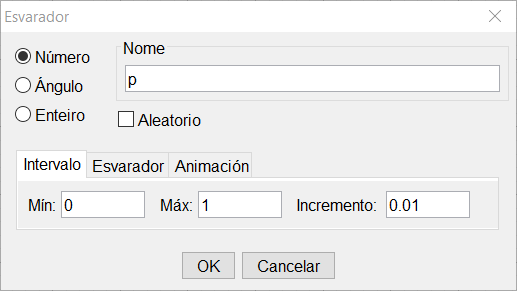
  • Crea outro Esvarador para a probabilidade de éxito \(p\).

• Representa a función de masa correspondente: DistribuciónBinomial(n, p).
• É probable que, para unha mellor visualización, teñas que modificar a razón entre as escalas. O axuste dependerá do gusto de cada quen e da pantalla que uses; proba con cal o ves ti mellor.

• Movendo os esvaradores de forma dinámica podes explorar de forma intuitiva certas propiedades da distribución, coma o efecto que tería modificar os parámetros que a determinan ou a súa carencia de simetría.
• Co comando DistribuciónBinomial( <Número de ensaios>, <Probabilidade de éxito>, <Valor da variable>, <Acumula (Booleana)> ) podes resolver exercicios relacionados con distribucións binomiais. Proba por exemplo a calcular \(P(X=5)\) se \(X\sim Bin(15;0,2)\).

GeoGebra ofrece tamén unha vista para traballar especificamente con distribucións de probabilidade. De feito, seguramente resulte máis cómoda para realizar cálculos, pero a desvantaxe é que non permite traballar de forma dinámica cos esvaradores.

• Activa a Vista Cálculos de probabilidade.
• Selecciona a distribución Binomial e indica os valores de n e p.
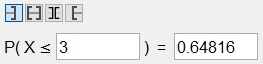
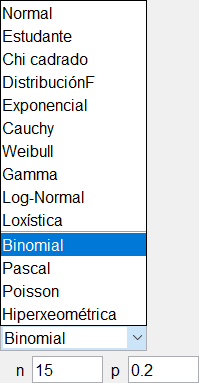• Selecciona o tipo de intervalo axeitado, e indica o valor numérico correspondente.

Exercicio de aplicación

Unha empresa de distribución de ovos véndeos por ducias. Ten estudado que o 5 % dos ovos chegan rotos ao comprador.

• Calcula a probabilidade de que, se compras unha caixa, non veña ningún roto.
• Calcula a probabilidade de que, se compras unha caixa, veñan rotos entre 1 e 3.
• Calcula a probabilidade de que, se compras unha caixa, veñan rotos máis de un.
• Calcula o número esperado de ovos rotos, e con que desviación típica.

Distribución normal

• Imos comezar por representar a función de masa de densidade dunha distribución continua como é a distribución normal \(N(\mu;\sigma)\).
  • Crea un Esvarador para a media \(\mu\) (podes chamarlle 'media') e outro Esvarador para a desviación típica \(\sigma\) (podes chamarlle 'desviacion').
  • Representa a función de densidade correspondente: DistribuciónNormal(media, desviacion, x, false). Se cambias false por true terás a función de distribución acumulada. É posible que, para unha mellor visualización, teñas que modificar a razón entre as escalas.
  • Movendo os esvaradores de forma dinámica podes explorar de forma intuitiva certas propiedades da distribución, como a súa simetría ou o efecto que tería modificar os parámetros que a determinan.
  • Activa a Vista Cálculos de probabilidade.
  • Selecciona a distribución Normal e indica os valores de \(\textcolor{blue}{\mu}\) e \(\textcolor{blue}{\sigma}\).
  • Selecciona o tipo de intervalo axeitado, e indica o valor numérico correspondente.

Exercicio de aplicación

O peso do alumnado de Bacharelato dun instituto segue unha distribución normal de media 75 kg e desviación típica 5. Elixida unha persoa ao azar, calcula a probabilidade de que:

• Teña un peso entre 80 e 82 kg.
• Teña un peso superior a 85,6 kg.
• Teña un peso inferior a 73 kg.
• Teña un peso entre 70 e 80 kg.

Aproximación da binomial pola normal

Como a distribución binomial se pode definir como a suma de \(n\) experimentos de Bernoulli independentes coa mesma media e varianza, é por tanto inmediato que podemos aplicar o teorema central do límite para un número suficientemente grande de experimentos. Partindo dunha distribución binomial \(Bin(n;p)\), esta ten media \(n\cdot p\) e desviación típica \(\sqrt{n\cdot p\cdot (1-p)}\), e o teorema permite asegurar que para \(n\) suficientemente grande se ten que \(Bin(n;p)\sim N(n\cdot p; \sqrt{n\cdot p\cdot (1-p)})\). Imos usar o GeoGebra para visualizar esta aproximación

• Crea dous Esvaradores, un para \(n\) (entre 1 e 200, de 1 en 1) e o outro para \(p\) (entre 0 e 1, de 0,01 en 0,01).
• Representa a función de masa da binomial: DistribuciónBinomial(n, p).
• Representa a función de densidade da normal: DistribuciónNormal(n p, sqrt(n p (1 - p)), x, false).
• É probable que, para unha mellor visualización, teñas que modificar a razón entre as escalas.
• Imos crear etiquetas para amosar cales son as distribucións. Para iso, na barra de ferramentas preme na icona Texto .
• Notas sobre os textos:
  • Se sabes LaTex podes empregalo para escribir en modo matemático. 
  • Para que no texto cambien de forma dinámica os parámetros que empregamos, tes que escribilos dentro dun recadro específico, premendo en Obxectos \(\rightarrow\) (caixa baleira).

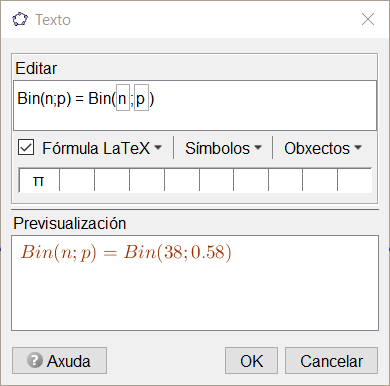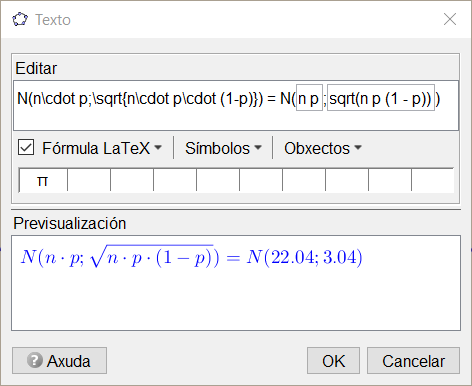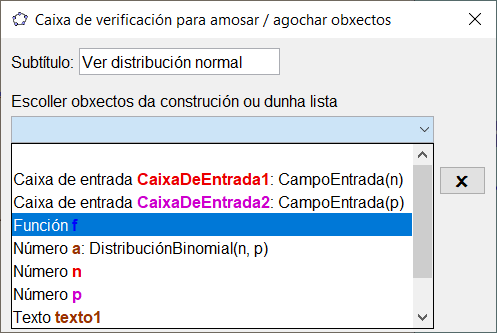
• Imos crear un botón que permita agochar/amosar a normal. Na barra de ferramentas preme na icona Caixa de verificación para amosar/agochar obxectos . Pon de subtítulo 'Ver distribución normal' e asócialle a función e o texto correspondentes.