Na Vista Alxébrica escribimos os extremos, por exemplo a=0, b=2.
Na Vista Gráfica inserimos dende o menú de iconas dúas Caixas de entrada 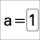, unha para cada extremo, escribindo o seu nome no Subtítulo e seleccionando o extremo correspondente no despregable de Obxecto vinculado.
Na Vista Alxébrica escribimos as rectas x=a e x=b. Dámoslle a mesma cor que ás caixas de entrada, e estilo punteado.
Escribimos a expresión analítica dunha función, por exemplo \(\sqrt{x^3+1}\).
Esta función non ten unha primitiva elemental. Podemos comprobalo mediante o comando Integral(f).
Creamos outra Caixa de entrada 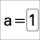para a función.
Inserimos un Esvarador 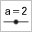de nome n, sendo un enteiro entre 2 e 50.
GeoGebra dispón de comandos específicos para a suma dos rectángulos, polo que escribimos directamente defecto = SumaInferior(abs(f(x)), a, b, n) e exceso = SumaSuperior(abs(f(x)), a, b, n).
Escribimos area = Integral(abs(f(x)), a, b) para que o programa nos devolva o valor da área buscada.
Damos tres cores distintas para cada un deses valores.
Na Vista Gráfica, para cada unha delas inserimos unha Caixa de verificación . Indicamos o subtítulo axeitado e escollemos o obxecto correspondente; unha vez creadas asignamos cores para relacionar cada caixa cunha área.
Inserimos un Texto . Preme na na opción Fórmula LaTex para escribir algo do estilo Exceso = \sum_{i=1}^n \dfrac{b-a}{n}\cdot f(x_i).
Creamos Textos tamén para visualizar na Vista Gráfica o resultado das aproximacións por rectángulos, a área e os erros cometidos. Para iso, na ferramenta de texto hai desplegar a opción Avanzado, premer na pestana e seleccionar (caixa baleira).
Podemos propoñer ao alumnado que explore con esta construción distintos intervalos e distintas funcións.
O applet pode reutilizarse e completarse co método dos trapecios, sen máis que escribir trapecios = SumaTrapezoidal(abs(f(x)), a, b, n) e engadir cores e textos convenientemente.

Actividade GeoGebra

https://www.geogebra.org/m/mcrbpkrh (Nova xanela)

Paulo%20Glez%20Ogando,https%3A//www.geogebra.org/m/mcrbpkrh,M%E9todo%20dos%20rect%E1ngulos%20e%20dos%20trapecios,1,Autor%EDa

Actividade%20non%20completada,Actividade%20superada.%20Puntuaci%F3n%3A%20%25s,Actividade%20non%20superada.%20Puntuaci%F3n%3A%20%25s,Gardar%20a%20puntuaci%F3n