O paradoxo de Braess

Algo que moito me fascina é o carácter abraiante dos paradoxos. Resultan chocantes, estraños e até incribles. Incluso en ocasións obrigan a que releamos o texto para convencernos de que realmente o que acabamos de ler ten algún sentido. Nas próximas liñas vai vostede ler sobre un deses que ao coñecelo deixa a cabeza abaneando coa impresión. Prepárese para coñecer o paradoxo de Braess.

Este paradoxo foi postulado por Dietrich Braess (n. 1938) no ano 1968, está relacionado co fluxo do tráfico e de forma resumida o seu enunciado é algo así: «engadir capacidade a unha rede pode, en ocasións, ralentizar o tráfico». Ou dito de outro modo, que nunha zona na cal o tráfico sufra conxestións, agregar un camiño novo non garante un mellor fluxo de vehículos, podendo incluso chegar a empeorar o tránsito. Sorprendente, ben si? Non sei a vostede, pero a min no seu día pareceume totalmente contraintuitivo.

Obviamente, o paradoxo de Braess non asegura que iso vai pasar, senón que pode pasar en situacións concretas. O cal xa me parece suficientemente estraño. Para tratar de entendelo, imos esculcar o argumento de Braess paso a paso, á vez que nos apoiamos nalgúns diagramas clarificadores. Comecemos por deseñar un modelo sinxelo, cun lugar de orixe e un punto de destino. Para percorrer esta ruta hai dous camiños posibles, un que pasa por un punto intermedio A e outro que o fai por B (figura 1).

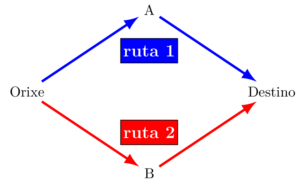
Para o caso que nos ocupa, que é entender o paradoxo, imos supoñer que ambos os camiños teñen a mesma lonxitude e, en xeral, que a escolla dun deles debería resultar indiferente. O único motivo que na práctica levaría a un conductor a decantarse por un ou outro sería a fluidez da circulación existente en cada un.

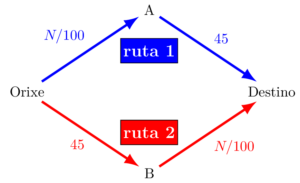
Suporemos tamén que hai dous tramos que corresponden con estradas de alta capacidade (unha autovía con varios carrís, por exemplo), o que vai da orixe a B e o que vai de A ao destino. Nestes a velocidade non depende do número de vehículos, sempre se tarda 45 minutos en completalos.

Porén, os outros dous tramos son estradas de baixa capacidade (unha nacional ou unha comarcal) nas cales os estudos feitos a partir dos datos recollidos por distintas medicións revelan que o tempo que tarda un coche en completalos si depende de cantos vehículos optaron por seguir ese camiño. Son o que vai da orixe a A e o que vai de B ao destino, e eses mesmos estudos conclúen que se hai N coches no tramo, lévalle N/100 minutos a cada un.

Seguiume vostede até aquí? Se se perdeu, na figura 2 ten un esquema da situación que consigna o tempo que tardaría un coche en percorrer cada un dos tramos.

Para continuar co noso modelo, imos partir da base de que son 4000 os vehículos que percorren esta ruta. Se todo o mundo ten sentidiño e se comporta racionalmente, 2000 irán pola ruta 1 e outros 2000 optarán pola ruta 2. Deste xeito, todos os coches tardan minutos en chegar ao destino.

Antes de chegar ao paso de engadir unha nova ruta, como suxería o enunciado inicial do paradoxo, imos convencernos de que a elección anterior (2000 para cada ruta) é a máis racional. Pensemos nalgunha outra opción, coma 2400 vehículos elixindo a ruta 1 e 1600 circulando pola ruta 2. Con esa distribución, os da ruta 1 tardarían minutos e os da ruta 2 tardarían minutos. Que sucedería? Pois seguramente tras unha conversa cun veciño ou cunha compañeira de traballo, quen empregou en chegar 69 minutos descubriría que existe unha ruta máis rápida a non moito tardar, e ao día seguinte cambiaría de ruta. E iso iría pasando sucesivamente até que o fluxo de ambas as rutas se equilibren, con 2000 vehículos en cada unha.

Unha vez convencidos de cal debe ser o reparto se todas as persoas actúan de xeito racional, o que imos facer é engadir un novo camiño. Ante a gran cantidade de coches que realizan este traxecto a diario, o concello decide realizar unha forte inversión para abrir unha rúa que une A con B, con carrís nos dous sentidos (pode circularse de A cara B, e tamén de B cara A). Na figura 3 ten o diagrama coa nova situación.

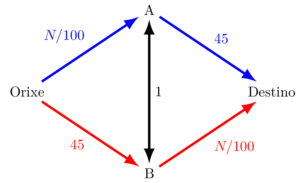
Para axudar a que vostede quede coa boca aberta, vou supoñer que este novo vial ten unhas condicións excelentes, tanto que todos os coches a poden percorrer en tan só un minuto de tempo. Que cre que vai pasar “grazas” a ela? Pénseo e estableza a súa propia hipótese antes de continuar… así a sorpresa será maior.

Situémonos na orixe e pensemos que tramo convén tomar. No peor dos casos, no cal todos os coches circulan pola estrada de baixa capacidade, o tempo que se tarda en chegar a A é de minutos. Se pola contra se parte cara B, tárdanse 45 minutos. Todas as persoas, lembremos que deciden racionalmente, van preferir ir cara A, xa que independentemente de cantos coches circulen por ese tramo vai supoñer menos tempo que ir cara B.

Chegados a A, hai dúas opcións. Ou ben se vai directamente ao destino, engadindo outros 45 minutos ao traxecto, ou ben se usa o novo vial no cal se tarda un só minuto, que no peor dos casos supón outros minutos.

Por tanto, a opción lóxica para os 400 vehículos é orixe → A → B → destino, que consume un total de minutos… que asombrosamente é bastante máis lenta que a que había antes da mellora. Quizais se vostede sufre atascos no seu camiño diario ao traballo, tiña que considerar en dirixir un escrito ás autoridades solicitando que pechen algunha estrada.

Ou non? Abraiante o paradoxo de Braess, non é? Resulta que os coches tardaban, en promedio, menos tempo cando o camiño entre A e B non existía que aproveitando o novo vial. No fondo deste paradoxo atópase a teoría de grafos, e tamén a teoría de xogos coa busca do que se coñece coma ‘punto de equilibrio de Nash’. No primeiro estado do modelo, antes da introdución do novo vial, que a estratexia de todas as persoas tenda a estabilizarse entre as dúas rutas con 2000 vehículos en cada unha e 65 minutos de tardanza para todos eles, é xustamente un equilibrio de Nash. E no segundo modelo, no cal xorde o paradoxo, o único equilibrio de Nash dáse coa estratexia analizada que conleva os 81 minutos de traxecto, xa que ningún coche se beneficiaría por cambiar a súa ruta.

É difícil atopar unha situación deste tipo na vida real, dada a enorme complexidade das rutas existentes na realidade. Pero si existen algúns exemplos coma o sucedido en Seúl, cando o derrubo dunha estrada de seis carrís levou á sorpresa a moitos profesionais xa que o fluxo do tráfico da cidade mellorou, no canto de empeorar (cóntao Linda Baker aquí). Non somos vostede e mais eu os únicos en mostrar estrañeza perante o paradoxo de Braess, non se vaia crer.

Algunhas referencias:

• Beveridge, Colin (2017). The maths behind… Discover the mathematics of everyday events. Cassell, London.

• Easley, David e Jon Kleinberg (2010). Networks, crowds and markets: Reasoning about a highly connected world. Cambridge University Press, Cambridge. Accesible na rede aquí.

• Paenza, Adrián (2018). ¡Un matemático ahí, por favor! Sudamericana, Buenos Aires.