O xogo do caos

Hai uns meses deume por ler ‘The mathematics that every secondary school math teacher needs to know’, de Alan Sultan e Alice F. Artzt. Unha lectura interesante, que non imprescindible, e que pode ser recomendable para persoas recentemente graduadas que estean dirixindo os seus pasos cara a docencia en secundaria, e tamén para profesorado de matemáticas que proveña doutras titulacións. Algo sempre se ha sacar en claro, aínda que só sexa dunha ollada a partes escollidas do libro.

Son 14 capítulos nos que se achega a multitude de temas relacionados coas matemáticas desa etapa. Como é obvio, ao non tratarse dun libro editado en España, a adaptación co noso currículo non é plena, pero si son moitos os contidos tratados que nós tamén temos. Por outra parte, hai algúns que nos caen lonxe, e outros que non sendo de aplicación directa si que sobrevoan o noso currículo, estando o suficientemente próximos ao que debemos traballar como para que cumpra coñecelos.

Eu deixo aí a referencia, e que cada quen decida se lle acae a lectura ou non. Pero recoméndolle a vostede que, como mínimo, bote un ollo ao índice. Malo será que algún tema non lle preste.

Ao que ía, eu viña aquí falar dunha cuestión concreta que non coñecía. Ou, como digo sempre nestes casos: se nalgún momento a coñecín, xa a esquecera. Que sabendo como é a miña memoria, ben puido ser o caso. Iso si, vou deixar claro que este contido cae precisamente no caixón dos (en España) extracurriculares. Poderiamos encaixalo nalgún lugar? Pois é posible, pero penso que o seu tratamento sería máis a modo de divulgación que de educación.

E non me quero ir polas ramas. Focalicemos: quero falar do xogo do caos. No libro preséntase no capítulo 8, nomeado ‘Indución, recursividade e dimensión fractal’, dentro do apartado 8.4, ‘Fractais revisitados e dimensión fractal’. Queda claro, non? A cousa vai de fractais.

As normas do xogo do caos son as que seguen:

• Comécese cun triángulo equilátero. Non importa o tamaño, pero que os tres lados sexan iguais. Imos etiquetar os tres vértices como A, B, C.

• A continuación, escóllase un punto P no triángulo, de forma totalmente aleatoria.

• Elixa un dos tres vértices A, B, C ao azar. Pode axudarse dalgunha ferramenta informática, ou dalgún tipo de buxaina con tres puntas. Unha recomendación: rescate dalgún caixón aqueles fidget spinner (figura 1) que se puxeran repentinamente de moda hai uns anos, etiquete cada punta, e a xirar!¹

• Se o spinner elixiu o vértice A, márquese o punto que está a medio camiño entre A e P. Igualmente se elixiu B ou C: márquese o punto medio entre P e o vértice elixido.

• Chámese 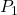a ese novo punto, e itérese o proceso: elíxase ao azar un dos tres vértices e márquese o punto medio entre o elixido e 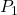. Así, unha e outra vez.

Antes de continuar, prégolle a vostede que repita o procedemento un feixe de veces, até que diante dos seus ollos vexa agromar unha regularidade na figura que, a ben seguro, aparecerá dentro do triángulo. Pode facelo con papel e lapis, ou pode axudarse dun ordenador. Pero fágame caso, inténteo antes de que eu lle conte nada máis. Se non ten vostede gana de enredar demasiado, pode practicar o xogo directamente nesta ligazón que preparei:

<https://www.geogebra.org/m/zebwz8qu>

Hai algo que está claro: o punto P inicial é aleatorio, non si? As “eleccións” do spinner son aleatorias, verdade? Por tanto, cabería agardar que a secuencia de puntos que imos xerando debería estar aleatoriamente disposta ao longo de todo o triángulo de partida, a que si? Pois non. NON. Como xa lle dixen, resulta que aparece unha regularidade, un padrón, algo parecido ao que se ve na figura 2. Para que se vexa ben, haberá que facer ducias de iteracións, se non centos. Quedará chulo se o fai cun ordenador, a man custaralle un bo anaco que se visualice con xeito.

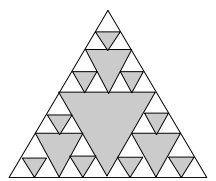
Efectivamente, é o triángulo de Sierpinski! É unha figura bastante coñecida, un dos fractais máis famosos², moi socorrido en obras de divulgación matemática. Pero independentemente de que sexa esta figura ou outra, de que vostede a coñecese xa ou a atope por primeira vez, o que chama a atención e deixa a un abraiado é que, xusto onde se podía esperar un resultado caótico, vai e aparece unha figura con moita regularidade? Fascinante.

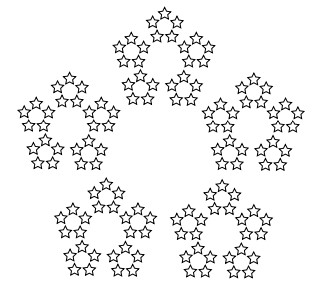
Por outra banda, a elección dun triángulo equilátero é puramente circunstancial. Ocorre o mesmo con outros polígonos. Tamén o é o feito de tomar o punto medio; as regularidades aparecen igualmente se é un terzo ou un sexto do camiño. Por exemplo, na figura 3 vese o padrón xerado a partir do pentágono regular e marcando de cada vez un punto a un terzo da distancia do vértice elixido ao azar. Iso si, para este o fidget spinner non serve de axuda… pero podería usar un dado do parchís. Dáse conta como?³

É máis, de usarmos como punto de partida unha disposición axeitada de 4 puntos no espazo, e irmos tomando de novo o punto medio en cada paso, obtense unha sorte de tetraedro de Sierpinski, o análogo tridimensional do triángulo de Sierpinski. Este tipo de procesos iterativos son moi comúns nas matemáticas. É máis, hai toda unha rama que se centra neles: a teoría de sistemas dinámicos discretos. Agora queda que faga vostede máis intentos, tanto variando o punto P coma a figura inicial e a distancia tomada. A xogar.

Referencias:

• Beltoforion <https://beltoforion.de/en/recreational_mathematics/chaos_game.php>.

• Sultan, Alan e Alice F. Artzt (2011). The mathematics that every secondary school math teacher needs to know. Routledge, Nova York.

• The Dynamical Systems and Technology Project at Boston University <https://math.bu.edu/DYSYS/chaos-game/node1.html>

• Wolfram MathWorld <https://mathworld.wolfram.com/ChaosGame.html>.