Cantos goles se marcan no fútbol

Non é doado predicir cantos goles se van marcar nun partido. Non obstante, non son moitas as opcións realista. Tampouco é sinxelo anticipar en que minuto se producirán. As casas de apostas lúcranse con estas circunstancias. Se vostede segue La Liga, lea as seguintes preguntas e detéñase a aventurar a súa resposta, baseada nas súas propias percepcións, antes de avanzar coa lectura. Cantos goles se marcan no fútbol? En cal das dúas metades dun partido se producen máis goles? Se dividimos a duración do encontro en intervalos de 15 minutos, en cal dos seis se anota máis goles?

Unha vez contestadas, a ser posible intentándoo sen consultar o dato real, é momento de continuar. Eu recompilei os datos de La Liga para a tempada 2024/2025, na que se marcaron un total de 995 goles. A figura 1 recolle os datos por metades: un 44,0 % dos goles marcáronse na primeira metade, un 56,0 % na segunda parte. Na figura 2 aparecen os datos por intervalos de 15 minutos: sucesivamente supoñen o 12,7 %, o 13,5 % e o 14,7 % na primeira parte, e o 14,8 %, o 17,1 % e o 16,2 % na segunda. Nos tempos de engadido tras os 45 minutos regulamentarios prodúcense o 3,1 % e o 7,9 %, respectivamente.

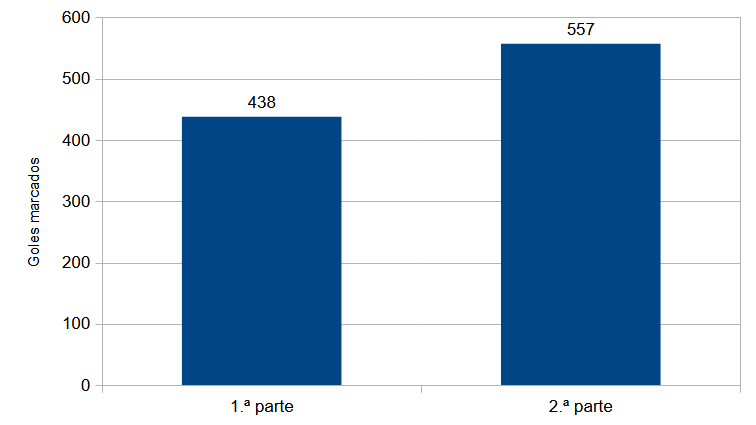
Figura 1. Goles anotados por metade, La Liga, 2024/2025. Datos tomados de Transfermarket.

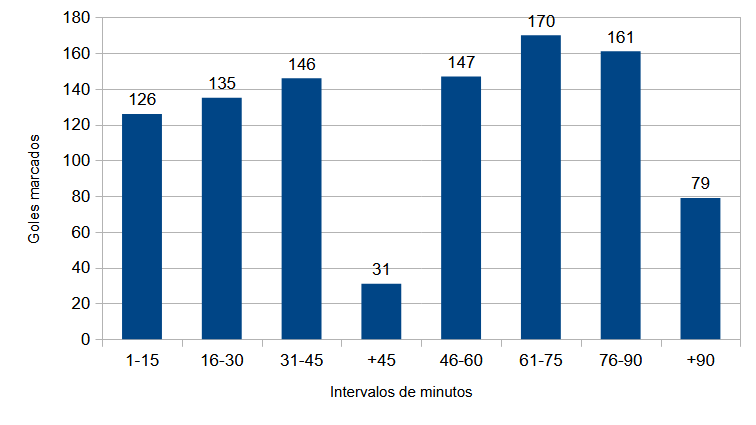
Figura 2. Goles anotados por intervalos de 15 minutos, La Liga. 2024/2025. Datos tomados de Transfermarket.

Á vista dos datos, semella que as segundas partes son máis goleadoras que as primeiras. Unha hipótese para explicar isto podería ser que os encontros comecen cunha fase de tenteo e a intensidade aumente xa na segunda parte, cos equipos esforzándose xa ao máximo. Mirando os datos por intervalos de 15 minutos obsérvase un crecemento case continuo, que só se racha no último dos seis intervalos, probablemente porque o cansazo é máximo.

O que máis chama a atención na figura 2 é o número de goles que se marcan nos tempos engadidos. O da primeira parte é notablemente baixo, e vou aventurar unha explicación: todo o mundo está pensando xa no período de descanso, en rearmarse de cara á segunda metade, e por iso os equipos son pouco incisivos. Igualmente, os árbitros tenden a engadir menos tempo ao final das primeiras partes que nas segundas, algo que ten o seu peso na comparación entre ambos os datos.

Especialmente significativo é o elevado número de goles conseguidos na prolongación da segunda metade, xa ao final do encontro. Acádase unha cantidade de tantos que supera á metade dos conseguidos en catro dos seis intervalos de 15 minutos, cando a media de minutos engadidos é inferior a 7,5 minutos. Probablemente se trate de que nos últimos intres xa non se contemporiza tanto, algúns equipos arriscan máis, os xogadores chegan ao seu límite e moitos partidos decídense neses instantes.

Estatisticamente, na gráfica dos goles anotados por intervalos de tempo non se aprecia aparentemente ningunha distribución específica. Pero, que ocorre de considerarmos os goles anotados por partido? A figura 3 recolle os datos ao respecto. O número de goles máis habitual foi tres, aínda que a diferenza é escasa cos partidos de un e de dous goles. O máximo foi de 8 goles, algo que só ocorreu en dúas ocasións. E só 21 dos 380 encontros remataron cun pírrico empate 0-0.

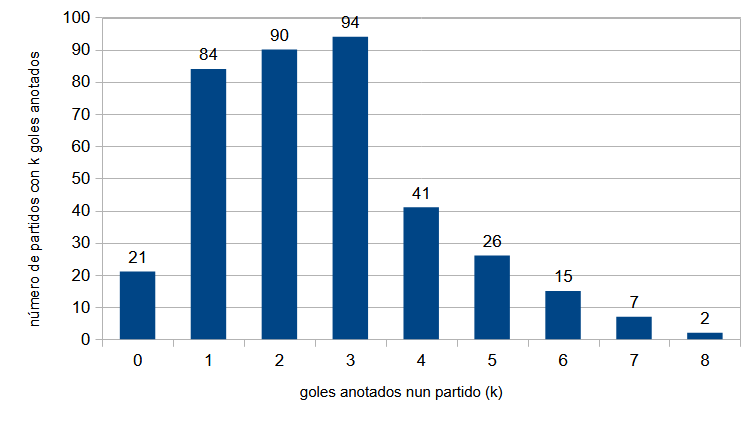
Figura 3. Número de partidos en La Liga na tempada 2024-2025 de acordo co número de goles anotados.

Porén, esta distribución dos datos si ten certo parecido cunha distribución de probabilidade moi empregada en estatística: a distribución de Poisson.

En 1838, Simeón Denis Poisson (1781 – 1840) propuxo unha distribución de probabilidade discreta que agroma cando se conta o número de ocorrencias dun determinado evento durante certo período de tempo. Entre os exemplos desta distribución pode pensarse no número de clientes que acoden a unha tenda diariamente, o número de chamadas que recibe o departamento de atención ao cliente nun día, o número de whatsapps que recibes nunha hora, o número de vehículos que soporta unha autoestrada cada día, o número de estrelas nun certa porción de espazo etc.

En resumo, as variables que seguen esta distribución son variables «de conteo». Basicamente, consideramos que esta distribución se deriva dun proceso experimental no que se observa a realización dun evento, con carácter aleatorio, durante certo período de tempo ou ao longo dun espazo de observación, e no cal se aprecian estas características:

O número de eventos que ocorren nun intervalo é independente do número que ocorre noutro intervalo disxunto.
A probabilidade de que un evento ocorra nun intervalo suficientemente pequeno é proporcional á lonxitude do devandito intervalo.
A probabilidade que ocorra máis de un evento nun intervalo suficientemente pequeno é desprezable.

Trátase dun modelo especialmente útil para contar sucesos que se dan con baixa frecuencia e de maneira aparentemente aleatoria. Baixo estas circunstancias, tómase a variable «número de eventos que se producen nun intervalo de tempo ou de espazo», que segue unha distribución de parámetro λ con esta función de masa de probabilidade:

$f(k) = P(X=k) = \dfrac{\lambda^k \cdot e^{-\lambda}}{k!}$ ,

onde X é o número de eventos, λ é o número medio de eventos por intervalo, $k\in \left\lbrace 0,1,2,\dots \right\rbrace$ e $k!$ é o factorial do número k, que se calcula facendo $k\cdot (k-1)\cdot (k-2)\cdot \dots \cdot 3\cdot 2\cdot 1$ .

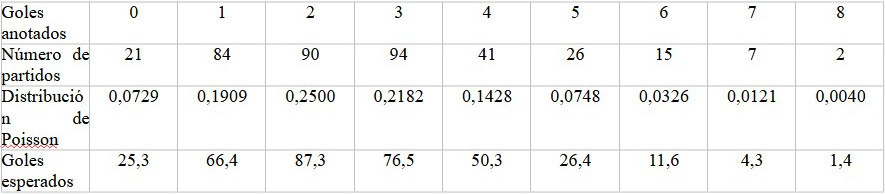
Táboa 1. Número de partidos en La Liga na tempada 2024-2025 de acordo co número de goles anotados.

Recollamos de novo os datos de goles por partido en La Liga 2024/2025 (táboa 1, segunda fila). É doado calcular a media: 995 goles en 380 supoñen aproximadamente 2,62 goles por partido. Ese é o valor que tomamos para λ, o número medio de goles por partido. Para $k\in \left\lbrace 0,1,2,3,4,5,6,7,8 \right\rbrace$ aplícase a fórmula anterior, resultando as probabilidades da terceira fila da táboa 1. Na cuarta fila da táboa 1, simplemente multiplicouse cada probabilidade polo total de partidos (380), obtendo o número agardado de partidos con k goles segundo a distribución de Poisson.

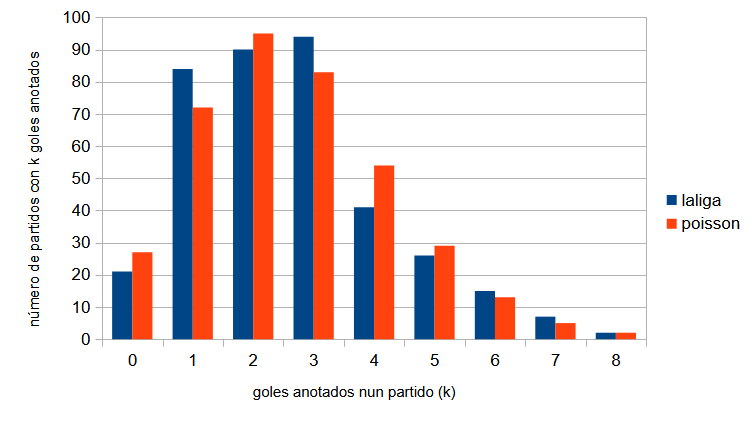
Os datos reais e os preditos por Poisson están representados a un tempo na figura 4. A similitude é notable, trátase dunha distribución moi próxima aos goles que realmente foron marcados. Para comparar a distribución observada (os datos reais dos goles) coas frecuencias esperadas baixo unha distribución de Poisson cun certo parámetro λ (a media de goles, que arredondando foi de 2,62), empreguei unha proba de bondade de axuste de chi-cadrado . Esta resultou un p-valor de 0,2336; ao ser maior que 0,05, non hai evidencia estatística para rexeitar que os datos seguen unha Poisson, o que significa que se trata dun modelo estatisticamente razoable para describir estes datos.

Figura 4. Número de partidos en La Liga (columnas azuis) na tempada 2024-2025 de acordo co número de goles anotados. As columnas en vermellos corresponden aos goles agardados segundo a distribución de Poisson.

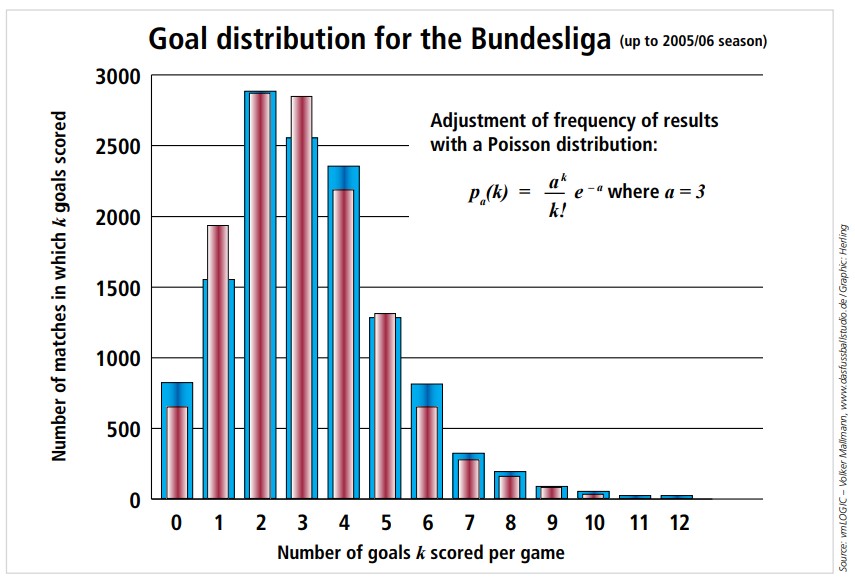
A idea de establecer este modelo, claro, non foi miña. Xa o fixo antes, por exemplo, Metin Tolan, analizando os datos da Bundesliga alemá na tempada 2005/2006. Os resultados que obtivo son moi semellantes (figura 5).

Obviamente, a correlación entre o modelo e os datos experimentais non é exacta, pero a distribución de Poisson é sorprendentemente próxima. Non deixa de ser un padrón aproximado, pero este tipo de resultados téñense comprobado empiricamente para varias ligas profesionais e para competicións de seleccións, así como tamén para equipos.

Figura 5. Distribución de goles por partido (en azul) na Bundesliga 2005/2006, en comparativa coa distribución de Poisson (en vermello). Fonte: Metin Tolan (2014).

Algunhas referencias:

Rojas González, Raúl (2022). El fútbol bajo el microscopio. La Ciencia para Todos, n.º 258, Cidade de México.
Tolan, Metin (2014). Germany for the World Cup? German Research, Magazine of the Deutsche Forschungsgemeinschaft, 1/2014.
As. <https://as.com/resultados/futbol/primera/calendario/>
Transfermarket. <https://www.transfermarkt.es/laliga/torverteilungminuten/wettbewerb/ES1/plus/1>

Deixa un comentario Cancelar a resposta