Halley, moito máis que un cometa

Se lle falo a vostede de Halley, a ben seguro que o primeiro que lle vén á cabeza é o cometa Halley: un corpo celeste que orbita arredor do Sol cada 75 anos, aproximadamente. A última vez que deu un paseo observable dende a Terra foi en 1986, e agardámolo de novo para 2061. A partir dunhas observación realizadas ao paso do cometa en 1682, Edmund Halley (1656 – 1742) empregou as leis do movemento de Isaac Newton (1643 – 1727) para ser o primeiro en calcular a órbita do cometa. Por iso é que na súa honra se lle puxo o seu nome a este cometa, probablemente o máis famoso da súa condición.

E xa que falamos de Newton, que sen dúbida ningunha é un dos científicos máis importantes da historia, podemos aproveitar para mencionar que precisamente Halley tivo a súa importancia na publicación de Philosophiæ naturalis principia mathematica, que é a obra máis importante que nos legou Newton. Foi Halley quen o animou e quen financiou parte da publicación, así que con isto a ciencia débelle unha, aínda que a súa participación fose indirecta. Newton foi o autor, o mérito é seu, pero un chisco do merecemento podemos concederllo a Halley.

O noso interese por este científico non acaba aí, e esta entrada imos dedicarlla a un apartado menos coñecido dos seus traballos. Ao bo de Edmund debémoslle un feixe de contribucións en astronomía, física e matemáticas, pero aquí imos explorar as matemáticas dos seguros, sobre as que escribiu un artigo en Philosophical Transactions, a revista da Royal Society, en 1693. Halley, moito máis que un cometa.

Nese artigo Halley asegura que a contemplación da mortalidade da humanidade ten, ademais dun uso moral, utilidades físicas e políticas. Entre estas últimas, menciona que xa foron sabiamente consideradas con anterioridade por Sir William Petty (1623 – 1687), nas súas Observacións Naturais e Políticas sobre os Rexistros de Mortalidade de Londres, atribuídas ao capitán John Graunt (1620 – 1674), así como posteriormente, nun tratado semellante sobre os rexistros de mortalidade de Dublín. Estes traballos foron pioneiros pero imperfectos, debido a que non se incluía a idade das persoas falecidas, e tamén pola profusión de forasteiros que chegaban a esas cidades e morrían alí.

Os métodos empregados por Petty e Graunt serviron como marco para o que sería a demografía moderna, pero a entidade de Halley como matemático era superior á dos seus predecesores, e a análise que el realizou foi de maior calidade. No mencionado artigo elaborou unha táboa de mortalidade da cidade de Breslavia, en Polonia (en polaco, Wrocław). A disposición de Halley estaban datos que recollían, mes a mes, tanto a idade coma o sexo de todas as persoas falecidas, en comparación co número de nacementos, durante os anos 1687, 1688, 1689, 1690 e 1691. En base a estes valores calculou a taxa anual de mortalidade e mais a mortalidade infantil, e elaborou tamén táboas (figuras 1 e 2) que logo se usaron durante anos para ofrecer rendas vitalicias e pólizas de seguros de vida.

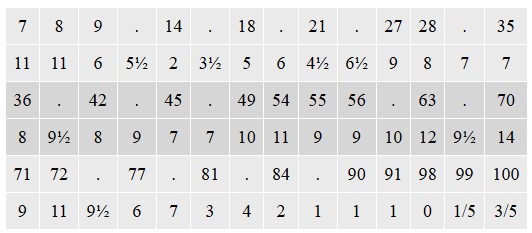
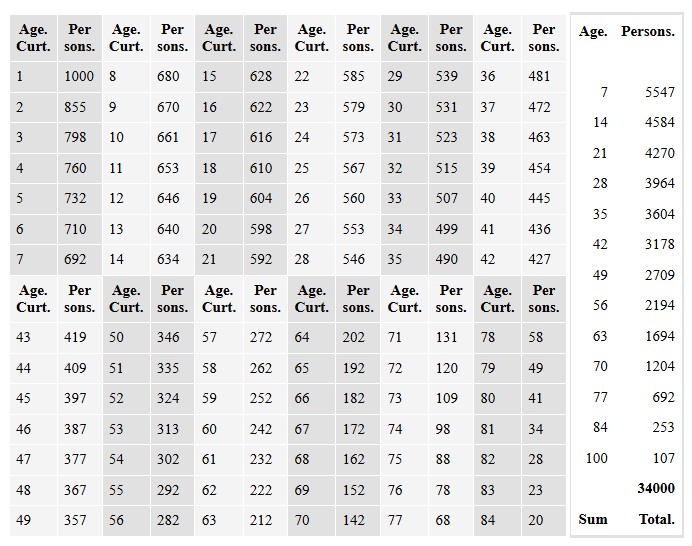
Son varias as análises que Halley realizou a partir das súas táboas. O primeiro uso é mostrar a proporción de homes capaces de portar armas dentro dunha multitude. O segundo uso é mostrar os distintos graos de mortalidade en todas as idades; ao dividir o número de persoas dunha certa idade que sobreviven despois dun ano pola diferenza entre ese número e o da idade proposta, obtéñense as probabilidades de que unha persoa desa idade non morra nun ano.

O terceiro uso é calcular a que anos é probable que unha persoa dunha certa idade morra: se se divide á metade o número de persoas vivas da idade proposta, atoparase na táboa a idade na que ese número se reduce á metade pola mortalidade; esa é a idade ata a cal é unha aposta igual que unha persoa da idade proposta chegue antes de morrer. O cuarto uso é descubrir a diferenza entre o prezo de asegurar a vida dun home de 20 anos e a dun home de 50, algo que permite regular o prezo dos seguros de vida.

Halley describe algúns usos máis, relacionados fundamentalmente coas rendas vitalicias, pero como non quero estenderme demasiado, vounos deixar de lado (pero inclúo a ligazón ao artigo de Halley nas referencias de máis abaixo). Agora quero centrarme nos seguros, posto que non deixan de ser unha comercialización da teoría de probabilidades. A empresa aseguradora aposta a que un determinado suceso non vai ocorrer, mentres que a persoa que contrata o seguro cobre as súas costas en caso de que si suceda. Ambas as partes vense na obriga de valorar baixo que condicións están dispostas a a sumir o seguro. Probabilidade pura e dura, detrás de cada seguro que se asina está un concepto estatístico: a esperanza matemática ou valor agardado, que pondera a probabilidade que se asigna á ocorrencia do suceso coa cantidade que se paga.

Para entender isto último imos cun exemplo: Alicia acaba de comprar un smartphone, do trinque, pola nada desprezable cantidade de 800 €. Ao ser tan caro, decide contratar un seguro contra roubos por se acaso. A compañía aseguradora, baseándose nas estatísticas de anos anteriores (número de aparellos vendidos, número de aparellos roubados), considera que a probabilidade de que lle rouben o móbil no prazo dun ano é do 2 %. Ofrécelle a Alicia estas condicións:

• Alicia abona 30 € por un ano.
• De producirse un roubo, a compañía paga 800 € cos que Alicia poderá facerse cun novo aparello.
• De non haber roubo ningún, a aseguradora non paga nada.

Nós imos analizar por que a empresa decide ofertar o seguro con estes números. Basicamente, está interesada nunha variable X que recolle a súa ganancia neta. Na táboa 1 recóllense todas as opcións, tendo en conta que de producirse o roubo, as perdas da empresa serán de €.

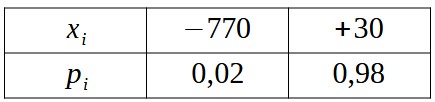
A esperanza matemática da variable X áchase mediante a fórmula . Neste caso o cálculo é moi doado: . É dicir, que a ganancia que pode agardar a aseguradora é de 14 € por cada cliente asegurado. Por suposto, haberá casos concretos nos que lle toque desembolsar unha cantidade considerable, pero a longo prazo gañará cartos. Se 1000 persoas contratan ese mesmo seguro, poden esperar facerse con 14 000 € ().

Esta análise é moi simple, a realidade é un pouco máis complexa. Porque claro, ponderar as probabilidades de ocorrencia de cada suceso susceptible de ser asegurado non é nada doado. É aí onde está o quid da cuestión: estimar as probabilidades, que é o que permite decidir cales son as cantidades a incluír no seguro para que a empresa saia gañando. De non contar cunha esperanza positiva, a aseguradora non ofrece seguro ningún.

Salvo erro pola súa parte, a nosa esperanza sempre será negativa. Por que pode compensar un seguro? Pois porque a empresa xoga coa lei dos grandes números: as poucas veces que lle toca pagar compénsaas coas moitas nas que se limita a cobrar a cota pactada. Pero no noso caso só somos un, e ou cobramos ou non. A cota debe ser unha cantidade asumible, da que esteamos en disposición de desprendernos, mentres que o abono en caso de ocorrencia do suceso debe ser substancioso, ou necesario para sacarnos dun apuro. Antes de asinar, debemos facer números e analizar todos os supostos. Ah, e moi importante tamén: ler sempre a letra pequena…

Algunhas referencias:

• Devlin, Keith (2008). The unfinished game. Basic Books, Nova York.

• Halley, Edmund (1693). An estimate of the degrees of the mortality of mankind. Philosophical Transactions, n.º 196, pp. 596-610.

• Hughes, David W. E Green, Daniel W. E. (2007). Halley’s first name: Edmond or Edmund. International Comet Quarterly, n.º 29, pp. 7-14. Accesible en liña: <http://www.icq.eps.harvard.edu/hughes_icq29_7t14.pdf>.

• Westfall, Richard S. (2006). Isaac Newton: una vida. Ediciones Akal, Madrid.