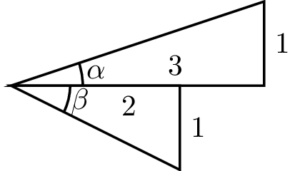
Antes de introducir os números de Gregory, partamos da figura 1. Ao situarnos no vértice da esquerda, hai un camiño ascendente e outro descendente; o ascendente ten pendente ![]() e o descendente ten pendente
e o descendente ten pendente ![]() . O obxectivo é achar o ángulo total entre ambos os camiños, é dicir, a medida do ángulo
. O obxectivo é achar o ángulo total entre ambos os camiños, é dicir, a medida do ángulo ![]() .
.
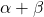 .
.Son dous triángulos rectángulos, polo que podemos aplicar as razóns trigonométricas. Ao coñecermos os catetos, usamos a tanxente. Pode vostede botar man dunha calculadora e comprobar os cálculos.
| Graos | Radiáns | |
|---|---|---|
Pode causar sorpresa o feito de ser exactamente 45º a medida de ![]() . Isto queda máis claro á vista da figura 2, na que se trazan unhas cantas liñas máis, de forma que o ángulo
. Isto queda máis claro á vista da figura 2, na que se trazan unhas cantas liñas máis, de forma que o ángulo ![]() resulta ser o que forma a diagonal dun cadrado co seu lado. Ao mesmo tempo, resulta que
resulta ser o que forma a diagonal dun cadrado co seu lado. Ao mesmo tempo, resulta que ![]() , un cálculo que corresponde cunha pendente de
, un cálculo que corresponde cunha pendente de ![]() .
.
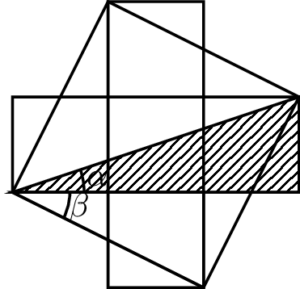
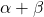 mide exactamente 45º.
mide exactamente 45º.Todo isto permite pensar nos ángulos xerados ao tomar unha pendente ![]() . Denotemos os devanditos números por
. Denotemos os devanditos números por ![]() , e escribirémolos en radiáns. Deste xeito, a relación anterior pode expresarse como
, e escribirémolos en radiáns. Deste xeito, a relación anterior pode expresarse como ![]() , unha fórmula xa coñecida por Leonhard Euler (1707 – 1783).
, unha fórmula xa coñecida por Leonhard Euler (1707 – 1783).
En 1980 Stephen Stiegler (n. 1941) enunciou o axioma que se coñece polo nome de Lei de Stiegler: «ningún descubrimento científico recibe o nome de quen o descubriu en primeiro lugar». Se ben non cabe dúbida de que se trata dunha esaxeración, tamén cómpre recoñecer que son moitos os achados que a verifican. Velaquí un bo exemplo da lei de Stiegler: en 1671 James Gregory (1638 – 1675) deu a expansión en series de potencias de sete funcións, entre elas a da tanxente e a da secante. Basicamente, Gregory descubriu as series de Taylor antes de que Brook Taylor (1685 – 1731), de quen toman o nome, as introducise en 1715. Outra das series expostas por Gregory foi precisamente a do arco tanxente:
![Rendered by QuickLaTeX.com \[\arctan(x) = x - \dfrac{x^3}{3} + \dfrac{x^5}{5} - \dfrac{x^7}{7}\cdots = \sum_{k=0}^{\infty} \dfrac{(-1)^k x^{2k+1}}{2k+1}\]](https://paulo.gal/wp-content/ql-cache/quicklatex.com-bd57ef2fcad4082cf420b2ec18eb58d6_l3.png)
O número ![]() do que falamos antes era xustamente
do que falamos antes era xustamente ![]() , o que nos brinda unha aproximación para o número
, o que nos brinda unha aproximación para o número ![]() que se adoita coñecer polo nome de fórmula de Leibniz. É ben fermosa, aínda que pouco eficiente porque converxe con bastante lentitude; precisa miles de termos para obter só catro decimais de
que se adoita coñecer polo nome de fórmula de Leibniz. É ben fermosa, aínda que pouco eficiente porque converxe con bastante lentitude; precisa miles de termos para obter só catro decimais de ![]() . Velaquí está:
. Velaquí está:
![]()
No problema inicial desta entrada estabamos interesados nas pendentes ![]() , é dicir, no resultado de
, é dicir, no resultado de ![]() . A serie anterior de Gregory permite obter outra serie para isto:
. A serie anterior de Gregory permite obter outra serie para isto:
![]()
Retomando a relación ![]() , e aplicando esta serie, temos unha nova aproximación para
, e aplicando esta serie, temos unha nova aproximación para ![]() , que converxe moito máis rápido que a anterior, pois é suficiente cos seguintes termos para chegar ao cuarto decimal:
, que converxe moito máis rápido que a anterior, pois é suficiente cos seguintes termos para chegar ao cuarto decimal:
![]()
Chegou o momento de xeneralizar, e á tanxente inversa de ![]() , sendo x un número racional, chámaselle o número de Gregory
, sendo x un número racional, chámaselle o número de Gregory ![]() . Tense así que
. Tense así que ![]() , e os valores
, e os valores ![]() mencionados antes son, pois, números de Gregory.
mencionados antes son, pois, números de Gregory.
Dixemos antes que xa Euler sabía que ![]() . Pero non quedou aí (Euler nunca “quedaba aí”): obtivo varias fórmulas para
. Pero non quedou aí (Euler nunca “quedaba aí”): obtivo varias fórmulas para ![]() empregando os números de Gregory, usando outras relacións coma
empregando os números de Gregory, usando outras relacións coma ![]() . Non foi o único. A maior contribución de John Machin (1680 – 1751) ás matemáticas a ben seguro que é precisamente o desenvolvemento dunha serie converxente para aproximar
. Non foi o único. A maior contribución de John Machin (1680 – 1751) ás matemáticas a ben seguro que é precisamente o desenvolvemento dunha serie converxente para aproximar ![]() . En 1706 calculou 100 díxitos decimais mediante a fórmula
. En 1706 calculou 100 díxitos decimais mediante a fórmula ![]() .
.
Esta última fórmula permite asegurar que existe máis dunha forma de expresar ![]() como combinación lineal de outros números
como combinación lineal de outros números ![]() . Porén, demostrouse que todo número de Gregory se pode expresar de forma única como unha combinación lineal de números
. Porén, demostrouse que todo número de Gregory se pode expresar de forma única como unha combinación lineal de números ![]() , sendo os índices n os números de Størmer. Como? Que? Números de Størmer? Que raio é iso?
, sendo os índices n os números de Størmer. Como? Que? Números de Størmer? Que raio é iso?
Imos con outra definición: os números de Størmer son os enteiros positivos n para os cales o maior factor primo p de ![]() é maior ou igual que
é maior ou igual que ![]() . Os primeiros números de Størmer son
. Os primeiros números de Størmer son ![]() . Como non podía ser doutro xeito, os números de Størmer teñen entrada propia na Enciclopedia En Liña de Series de Enteiros (OEIS). Debémosllos a Fredrik Carl Størmer (1874 – 1957), e antes de continuar voulle contar que unha fórmula debullada por el,
. Como non podía ser doutro xeito, os números de Størmer teñen entrada propia na Enciclopedia En Liña de Series de Enteiros (OEIS). Debémosllos a Fredrik Carl Størmer (1874 – 1957), e antes de continuar voulle contar que unha fórmula debullada por el, ![]() , foi empregada en 2002 por Yasumasa Kanada (1949 – 2020) para calcular a nada desprezable cantidade de 1 241 100 000 000 díxitos decimais de π. Aí queda iso. Non lle recomendo que tente escribilos todos, non.
, foi empregada en 2002 por Yasumasa Kanada (1949 – 2020) para calcular a nada desprezable cantidade de 1 241 100 000 000 díxitos decimais de π. Aí queda iso. Non lle recomendo que tente escribilos todos, non.
Retomemos o fío, e non quero que se me perda vostede con esta nova definición que acabamos de dar. Fíxese na lista: o 6 aparece, o 7 non. Por que?
-
Se
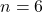 , calculamos
, calculamos 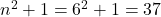 . O maior factor primo de 37 é o propio 37. E como
. O maior factor primo de 37 é o propio 37. E como 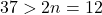 , tense que o 6 é un número de Størmer.
, tense que o 6 é un número de Størmer. -
Se
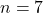 , calculamos
, calculamos 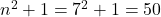 . O maior factor primo de 50 é o 5. E como
. O maior factor primo de 50 é o 5. E como 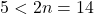 , tense que o 7 non é un número de Størmer.
, tense que o 7 non é un número de Størmer.
Non lle parece asombrosa a relación entre os números de Gregory e os números de Størmer? Pois terme das orellas, que vai ficar pampo: tamén teñen que ver cos números complexos, máis concretamente cos enteiros gaussianos, que son os complexos ![]() tales que
tales que ![]() son enteiros. O ángulo
son enteiros. O ángulo ![]() , correspondente cunha pendente
, correspondente cunha pendente ![]() , coincide co ángulo que determina o enteiro gaussiano
, coincide co ángulo que determina o enteiro gaussiano ![]() (que adoitamos chamar argumento). Desta maneira,
(que adoitamos chamar argumento). Desta maneira, ![]() está asociado co complexo
está asociado co complexo ![]() .
.
E de aí resulta que para atopar a combinación lineal dun número de Gregory en función de números de Størmer, multiplícase repetidamente ![]() por números
por números ![]() , sendo n un número de Størmer escollido para que se poidan cancelar factores primos p. Para isto, n debe ser o máis pequeno para o cal
, sendo n un número de Størmer escollido para que se poidan cancelar factores primos p. Para isto, n debe ser o máis pequeno para o cal ![]() é divisible por p.
é divisible por p.
Conway e Guy (non o dixera aínda, pero quero que quede claro: é nesa referencia onde aprendín todo isto) exemplifícano con ![]() , que corresponde co enteiro gaussiano
, que corresponde co enteiro gaussiano ![]() . Empezamos por comprobar se o 70 é un número de Størmer, pois se o fose nada disto faría falla; como
. Empezamos por comprobar se o 70 é un número de Størmer, pois se o fose nada disto faría falla; como ![]() , o maior factor primo é 29, e ao cumprirse que
, o maior factor primo é 29, e ao cumprirse que ![]() concluímos que non o é. Daquela, cómpre buscar a descomposición.
concluímos que non o é. Daquela, cómpre buscar a descomposición.
Buscamos agora o número n máis pequeno tal que ![]() sexa divisible por 29. Resulta ser o 12, que si é un número de Størmer (non se fíe de velo na lista de antes, compróbeo vostede). Entón:
sexa divisible por 29. Resulta ser o 12, que si é un número de Størmer (non se fíe de velo na lista de antes, compróbeo vostede). Entón:
![]()
O argumento de ![]() é
é ![]() , o de
, o de ![]() é
é ![]() , medido en sentido contrario. E podemos aplicar as propiedades dos números complexos, que neste caso nos din que a multiplicación de dous complexos resulta ter por argumento a suma dos argumentos dos dous números multiplicados. Igualmente, multiplicar un escalar (por 29, neste caso) simplemente modifica o módulo, polo que non afecta ao argumento. É dicir, que
, medido en sentido contrario. E podemos aplicar as propiedades dos números complexos, que neste caso nos din que a multiplicación de dous complexos resulta ter por argumento a suma dos argumentos dos dous números multiplicados. Igualmente, multiplicar un escalar (por 29, neste caso) simplemente modifica o módulo, polo que non afecta ao argumento. É dicir, que ![]() .
.
O outro factor primo de ![]() era 13, polo que para seguir co proceso buscamos o número n máis pequeno tal que
era 13, polo que para seguir co proceso buscamos o número n máis pequeno tal que ![]() sexa divisible por 13. É o 5, de novo un número de Størmer. Por tanto:
sexa divisible por 13. É o 5, de novo un número de Størmer. Por tanto:
![]()
Con isto tense que ![]() . Repetindo multiplicación chegamos a
. Repetindo multiplicación chegamos a ![]() , sendo 2 tamén un número de Størmer.
, sendo 2 tamén un número de Størmer.
![]()
que nos brinda ![]() .
.
Substituíndo axeitadamente todas as expresións anteriores e despexando, obtense que ![]() , que é a única combinación lineal do número de Gregory
, que é a única combinación lineal do número de Gregory ![]() a partir de outros
a partir de outros ![]() de tal xeito que todos os n sexan números de Størmer, como son 12, 5 e 2. Fabuloso. Na páxina 247 de The Book of Numbers pode consultar vostede as descomposicións (recorde, en cada caso é única) para os primeiros
de tal xeito que todos os n sexan números de Størmer, como son 12, 5 e 2. Fabuloso. Na páxina 247 de The Book of Numbers pode consultar vostede as descomposicións (recorde, en cada caso é única) para os primeiros ![]() até
até ![]() nos que n non é el mesmo un número de Størmer.
nos que n non é el mesmo un número de Størmer.
Algunhas referencias:
-
Conway, J. H. e Guy, Richard K. (1996). The Book of Numbers, Springer-Verlag, Nova York.
-
Data Science Parichay. <https://datascienceparichay.com/super-computing/pi-current/>
-
MacTutor. <https://mathshistory.st-andrews.ac.uk/Biographies/Gregory/>
-
Wolfram Mathworld. <https://mathworld.wolfram.com/GregoryNumber.html> e <https://mathworld.wolfram.com/StormerNumber.html>