O paradoxo da área do triángulo

Moito dubidei con este apartado á hora de etiquetalo, pois non sabía se incluílo cos paradoxos ou cos entretementos xeométricos. Tanto ten, no fondo, como clasifiquemos este paradoxo da área do triángulo, pois en todo caso o peor que pode ocorrer é… que teñamos dobre diversión!

Ben, en realidade, se nos poñemos técnicos, este paradoxo da área do triángulo non é un paradoxo. Se por tal cousa entendemos unha afirmación en aparencia verdadeira que inclúe unha autocontradición lóxica, podemos descartar que se trate dunha situación dese tipo, xa que unha análise concienciuda (máis ben, uns poucos cálculos) convéncenos enseguida de por que os ollos nos enganan nun primeiro momento.

De todos os xeitos, a situación vai seguir o mesmo esquema tipo de outros paradoxos dos que temos falado aquí: formulación do problema – sorpresa, sorpresa, como demos pode ocorrer iso? – explicación. Así que vai no caixón dos paradoxos, basta con adoptar a máxima de “na miña casa, as miñas regras”. E se a vostede non lle gusta, non lea (ui, non quería dicir iso oh, non se me alporice, non se me marche, lea lea, que hai suficientes entradas para que algunha lle preste). Veña, que imos: velaquí o paradoxo da área do triángulo.

Antes de comezar, o que si é que nesta ocasión é obrigado que colla vostede lapis e papel. E velaquí un par de restricións a maiores: o papel debe ser cuadriculado, e ten que engadir unha regra á listaxe de material necesario. Eu agardo por vostede. Levántese, reúna todo iso e busque un lugar con espazo suficiente para poñerse a debuxar.

Xa o ten todo? Pois imos aló. Siga comigo estes pasos, un por un. Eu irei acompañando o texto de imaxes para facilitarlle o seguimento do choio.

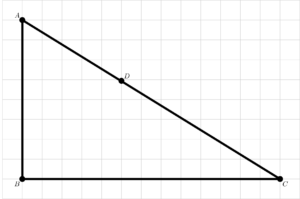
• Na parte superior esquerda da folla de papel cuadriculado marque un vértice e etiquéteo coa letra A.

• Dende ese punto A, trace un segmento vertical até un vértice que denominará B, situado a 8 cadradiños de A.

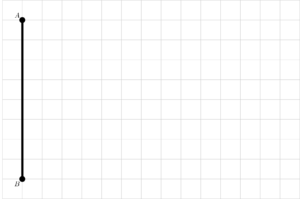
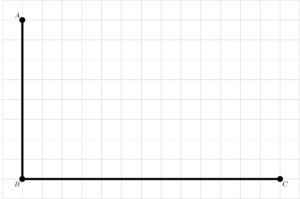
• A seguir, faga o mesmo dende o punto B cara a dereita, até un vértice que chamará C, situado a 13 cadradiños de B.

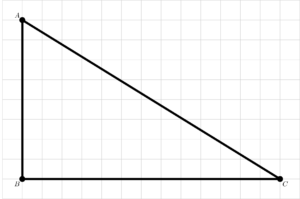
• Use a regra para unir, mediante un segmento, os puntos A e C.

• Verdade que o segmento AC pasa por un vértice da cuadrícula situado 5 cadradiños á dereita de AB e 5 cadradiños por enriba de BC? Chame D ao devandito punto.

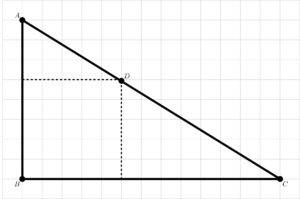
Con todo iso, a construción xa está basicamente lista. A continuación pasamos a labores de cálculos. Son poucos, non se me asuste. Ache a área do triángulo ABC de dúas maneiras distintas: a primeira directamente coa fórmula típica da área para o triángulo ABC, e a segunda axudándose do punto D, descompoñendo a figura en dous triángulos máis pequenos e un cadrado.

E xa estaría. Compare os dous resultados obtidos para a área. Nota algo estraño? A que pensa que se pode deber? Acaso unha das dúas formas de calcular a área era incorrecta? Por se acaso, imos revisar os cálculos.

1. A fórmula máis habitual para a área dun triángulo é 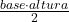. Neste caso a base mide 13 unidades e a altura 8, polo cal a área queda de 52 unidades cadradas.

2. O cadrado que aparece na figura 6 ten un lado de 5 unidades, polo que a súa área é de 25 unidades cadradas. Atendendo á fórmula do punto anterior, a área do triángulo inferior é 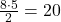unidades cadradas, mentres que a área do triángulo superior é 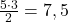unidades cadradas. Así, a área totaliza 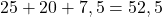unidades cadradas.

Neste mesmo blog, hai xa un tempo, dedicamos unha entrada precisamente á área do triángulo. Pode vostede revisitala nesta ligazón. E si, os cálculos son correctos. Teñen resultados diferentes pero, por que? A que se debe? Hai trampa?

Pois claro que hai trampa. Xa lle dicía ao comezo que probablemente esta situación non mereza o cualificativo de paradoxo (pero que aquí entre nós si que imos manter esa denominación). O quid da cuestión está no quinto paso, na figura 6. Aínda que a simple vista resulta natural afirmar que o punto D xace sobre un vértice da cuadrícula, a realidade é que cae moi próximo… pero non xusto sobre el. Pero a diferenza é moi pequena, e o habitual é que o ollo nos infunda suficiente confianza como para non dubidar de que o punto D pertence ao segmento AC.

Os dous resultados distintos puxéronnos sobre a pista de que algo fallaba na construción, constitúen unha evidencia de que algo non foi ben. Porén, salvo que coñezamos esta situación de antemán (ou algunha semellante), é raro que as dúbidas se dirixan cara o punto D. Tiremos unha ensinanza de todo isto: non sempre se pode confiar plenamente na nosa percepción visual. É algo que serve para crear e mais para intuír, pero non para demostrar. Usémola pero, ao mesmo tempo, sexamos críticos e complementemos o noso argumento cunha análise máis profunda.

O paradoxo da área do triángulo que presento aquí é bastante coñecido, e é posible que vostede xa o coñecese. Se non nesta versión, si nalgunha outra coma a que pode descubrir nesta ligazón. O que me gusta da versión que presento é a sinxeleza da súa construción, é moi rápido e doado facer isto con calquera persoa, e ver se abraia ou cae na conta do enredo.