O ‘x’ como incógnita

por

O uso da letra x como incógnita nas matemáticas e máis concretamente na álxebra é unha desas cuestións que transcenden esa ciencia. Moitas persoas poden non recordar gran cousa das matemáticas que estudaron na escola nin terse achegado a elas dende entón, pero por moitos anos que pasasen rapidamente asocian o x coas matemáticas.

Lendo a novela Samarcanda de Amin Maalouf (n. 1949) un pode ler o seguinte parágrafo: <<Durante os meses seguintes comenza a redacción dun libro moi importante consagrado ás ecuacións cúbicas. Para presentar a incógnita nese tratado de álxebra, Khayyam emprega o termo árabe shay, que significa ‘cousa’; esta palabra, escrita xay nas obras científicas españolas, foi reemprazada progresivamente pola súa primeira letra, x, que se converteu no símbolo universal da incógnita>>.1

Omar Khayyam (1048 – 1131) foi un científico e poeta persa, ademais dun dos protagonistas da novela Samarcanda. Foi el entón o primeiro en chamar x á incógnita? Pois… resulta que non está de todo claro, non hai evidencias de que esa explicación sexa a correcta. De xeito similar, tamén a palabra grega para ‘descoñecido’, xenos, comeza por x, e son así varias as teorías que establecen que o convenio podería ter nacido simplemente para abreviar unha palabra con significado relacionado cos problemas de álxebra.

Recentemente Terry Moore2 impartiu unha charla TED3 na que presentaba unha explicación semellante. Durante a Idade Media as matemáticas árabes eran as máis prósperas, e a vía de entrada en Europa duns cantos libros científicos foi España. Segundo Moore, os estudosos españois tiñan dificultades con certos sons árabes coma o correspondente á letra sheen. En obras matemáticas aparecía a palabra al-shalan para referirse a unha cousa descoñecida, e ao non haber un son que correspondese con sh, optaron polo son ck, que no alfabeto grego corresponde con chi, χ. Máis tarde nas traducións ao latín o χ sería reemprazado pola letra latina x… e xa non se cambiaría dende entón até os libros de textos actuais. O ‘x’ como incógnita que todo o mundo coñece hoxe.

A explicación de Moore é mera especulación, ao igual que a de Maalouf con Khayyam. Non están sostidas por evidencias documentais directas, e por tanto non son realmente demostrables. Se esiximos unha evidencia da cal si se garde rexistro escrito, hai que avanzar un pouco máis no tempo, até o século XVII, onde atopamos a René Descartes (1596 – 1650, figura 1). É posible que este tomase prestado o uso de x de outros, a verdade é que non se sabe, pero en todo caso é a aparición máis antiga que está documentada. E como mínimo si podemos recoñecer, e supoño que incluso agradecer, que foi el que popularizou o x como incógnita e favoreceu que se espallase esta notación que hoxe nos resulta natural.

O porqué de usar o 'x' como incóngnita. René Descartes
Figura 1. Retrato de René Descartes por Frans Hals.
Fonte: Wikimedia Commons.

Descartes usou o x como incógnita nos seus textos xa dende o ano 1629. Non se ten ningunha certeza do motivo polo cal se decidiu por facer esa escolla, pero a teoría máis plausible é que se debeu ao encargado da imprenta, xa que o x era a letra menos usada e por iso tiña máis bloques dispoñibles para o seu uso na imprenta.

Pero Descartes non se quedou aí, e tamén utilizou outras letras coma y ou z para representar diferentes cantidades. Na súa obra máis imporante, La Géométrie (1637), estableceu a notación pola cal se empregan as últimas letras do abecedario (x, y, z) para cantidades descoñecidas e as primerias (a, b, c) para cantidades coñecidas. E así seguimos, unhas asócianse habitualmente con incógnitas e as outras con parámetros.

E non só iso, pois a Descartes seguramente tamén debemos a notación actual para as potencias, nas cales colocamos o expoñente nun superíndice á dereita, coma por exemplo en x^4. Este convenio foi orixinalmente proposto por Nicolas Chuquet (1445 – 1488), pero a idea non cristalizou até que a retomou Descartes, e foi a partir de aí que a notación se impuxo. Cunha pequena diferenza, e é que para a potencia segunda Descartes seguía escribindo xx no canto de x^2, seguramente porque esta última non representaba ningunha vantaxe tipográfica, mentres que x^5 si era preferible a xxxxx.

Seguindo con Descartes e a súa obra La Géométrie, foi aí cando introduciu o que acabaría sendo coñecido como coordenadas cartesianas. Dúas rectas perpendiculares chamadas eixes que permitiron relacionar a xeometría coa álxebra, pois a unha figura xeométrica correspóndelle unha ecuación alxébrica, e así un pode traducir problemas e técnicas dunha desas ramas á outra segundo sexa conveniente en cada momento. E velaí outro uso da letra x, que nomea ao eixe horizontal mentres o y se destina ao eixe vertical.

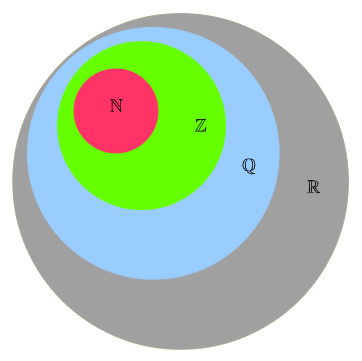
Árabe, grego, latín, francés… son moitos os idiomas que teñen influencia nas matemáticas. Todos os símbolos que emprega esta ciencia teñen a súa propia historia, que con frecuencia non aparece nas aulas. Os estudantes len, escriben, usan moitos símbolos dos cales é unha mágoa que descoñezan a súa procedencia, asumindo que non hai tempo para todo. Uns que aparecen con frecuencia durante a secundaria son os conxuntos numéricos (figura 2), aos que facemos referencia mediante as letras maiúsculas \mathbb{N} (para os números naturais), \mathbb{Z} (números enteiros), \mathbb{Q} (racionais) e \mathbb{R} (reais).

O porqué de usar o 'x' como incógnita. Conxuntos numéricos
Figura 2. Conxuntos numéricos.

Cando consulto ao alumnado sobre a posible orixe de cada unha desas letras, a resposta que agroma ao instante é «\mathbb{N} de natural» e «\mathbb{R} de real». E si, os tiros van por aí, aínda que non son o castelán nin o galego os idiomas dos que se tomaron. Pero \mathbb{Q} e mais \mathbb{Z} son outra historia, e adoitan provocar un silencio sepulcral que ninguén atina a romper para aventurar algunha explicación.

Pois ben, resulta que \mathbb{Q} provén… do italiano, sendo Guiseppe Peano (1858 – 1932) quen o usou por primeira vez no ano 1895 a partir da palabra quoziente, que significa cociente (noutros idiomas coma o alemán ou o inglés tamén comeza por q, quotient). Foi o mesmo Peano quen en 1895 introduciu tamén o \mathbb{N} por naturale, a palabra italiana para naturais.

O \mathbb{Z}, por outro lado, seica se debe ao grupo N. Bourbaki (pseudónimo dun grupo de matemáticos franceses da primeira metade do século XX) que a tomou da palabra alemana Zahlen, que significa números. E por último \mathbb{R} é o que menos misterio ten: inglés, francés, alemán, castelán, galego… en todos eses idiomas a palabra ‘real’ é parecida e en todos eles comeza pola letra r, así que neste caso a explicación é a evidente, o cal nos deixa que o alumnado soe acertar en dous dos catro casos.

Se vostede ten interese por coñecer de onde veñen símbolos máis habituais que se empregan nas matemáticas (que son moitos, verdadeiramente), permítome recomendarlle a obra de José Nicanor Alonso e Miguel Ángel Mirás que referencio a continuación. É o seu un fenomenal labor de recompilación sobre a súa orixe e evolución, e ademais é en galego!

Algunhas referencias:

  • Alonso Álvarez, José Nicanor e Mirás Calvo, Miguel Ángel (2019). Mate-glifos. Orixe e evolución dos símbolos en Matemáticas. Edicións Xerais, Vigo.
  • Blevins, Melissa. “The origins of the mathematical convention of using ‘x’ as the unknown”. Recuperado o 27/08/2023 desta ligazón.
  • Joyner, David (2008). Adventures in group theory. The John Hopkins University Press, Baltimore.
  • Maalouf, Amin (1989). Samarcanda. Alianza, Madrid.
  • Simon, Jacques (2017). Banach, Fréchet, Hilbert and Neumann Spaces, volume 1. ISTE Ltd., London.

1 Tradución ao galego do autor a partir da tradución ao castelán de María Concepción García-Lomas.

2 Director de The Radius Foundation.

Deixa un comentario