Falacia da acusación

Hoxe volvemos aos xulgados, onde non hai moito estivemos xa acompañando a Protágoras. Volvemos ás salas onde se imparte xustiza e nas cales unha ampla maioría da poboación confiamos con firmeza. Alí podemos atopar con certa frecuencia un erro estatístico coñecido polo nome de ‘a falacia da acusación’ ou ‘a falacia do fiscal’.

Podemos explicalo partindo da base de que, se o sospeitoso é inocente, a existencia dunha determinada evidencia ou proba é altamente improbable. Un dos exemplos máis típicos, sobre o que é sinxelo atopar bibliografía ao respecto, é o caso Sally Clark. A finais do século XX, os dous fillos desta muller morreron en circunstancias similares nun intervalo de pouco máis dun ano. Ela achacou ambos os falecementos ao síndrome da morte súbita do lactante (SMSL), pero acabou sendo condenada por dobre homicidio. Foi un caso no que confluíron diversos erros, algúns graves e non de índole matemática precisamente, e finalmente uns anos despois a condena foi anulada.

O que nos interesa nestas páxinas é a explicación da falacia. No caso Clark, certos cálculos indicaban que a probabilidade de que os dous nenos sufriran o SMSL era residual: en torno a 1 posibilidade entre 73 millóns. O razoamento incorrecto que se fai entón é asumir que se Clark fose inocente, a probabilidade de que ocorrese a dobre desgraza era tan baixa que necesariamente a explicación alternativa debería ser enormemente probable. Clark tiña que ser culpable.

Porén, esta deducción é incorrecta. Por un lado, asume a independencia de ambos os sucesos, cando por exemplo poderían deberse a factores xenéticos comúns. Cumpría unha análise forense máis detallada, e de feito este foi un dos motivos que levou á cancelación da condena no ano 2003. Por outra banda, non ten en conta a probabilidade de ocorrencia dun dobre asasinato infantil, da cal algúns cálculos conclúen que é incluso máis baixa, entre 4 e 9 veces menor que a do dobre SMSL. Cumpría sopesar máis detidamente a probabilidade relativa de ambas as dúas posibles explicacións, e non só a de unha delas como se fixo inicialmente.

Para aclarar este último punto, pense vostede nunha listaxe composta por algúns centos millóns de puntos, correspondendo cada punto cunha muller que tivo dous fillos. Coloréanse de vermello aqueles casos nos que houbo un dobre SMSL, e de amarelo aqueles nos que se deu un dobre asasinato. En verde aparecen os demais casos, que son practicamente todos. Pois ben, a probabilidade de que a nai sexa inocente é a razón entre o número de puntos vermellos e o número de puntos amarelos. Non sabemos cantos puntos vermellos e amarelos hai, pero si sabemos que o dato dos 73 millóns afástanos dunha análise correcta.

Esta falacia da acusación consiste pois no uso incorrecto -sexa ou non intencionado- da probabilidade condicional, de xeito que se mostra a probabilidade de que a acusada sexa inocente como extremadamente baixa, para concluír que a súa inocencia é case imposible. E ese uso incorrecto nace da confusión entre dúas probabilidades condicionadas que en realidade son ben diferentes.

Imos fixarnos un pouco máis nese dato de 1 posibilidade entre 73 millóns. É un número que se obtén a partir da declaración do experto pediatra Roy Meadow, que asegurou que a probabilidade de que un infante morra polo SMSL era de unha posibilidade entre 8543. Asumindo que as dúas mortes fosen independentes, iso brindaría unha posibilidade entre para o dobre SMSL. Arredondando, 73 millóns.

Con isto estamos, basicamente, ante a probabilidade de que ocorra o suceso condicionada á inocencia de Clark, algo que se denota (chámolle D aos datos comprobados, as probas recabadas, e I á inocencia da acusada) . Este tipo de probabilidades son as que poden presentar os expertos ou peritos no xuízo, que constitúen unha medida da incertidume en situacións nas que os feitos reais non son coñecidos con seguridade.

Non obstante, para tomar a súa decisión final, o xurado e o xuíz deben ter en conta a probabilidade de que a acusada sexa inocente, á vista das evidencias das que se dispón, que vén ser . Esta probabilidade non é a mesma que a anterior, baste pensar nestoutro exemplo extremo: non confunda vostede a probabilidade de que un animal teña catro patas, se sabe que é un elefante, , coa probabilidade de que sexa un elefante, se coñece que ten catro patas, . Pénseo vostede ben, estas últimas dúas medidas ofrecen cantidades moooi diferentes, e deixan ben clara a distinción entre ambas as probabilidades.

Para entender mellor esta falacia da acusación, tomemos o exemplo que explica Montes (2003): cometeuse un crime e hai 10 000 persoas que poderían ter sido culpables, das cales 200 traballan nun pozo mineiro. Na escena do delito atopáronse restos que só poden provir dese pozo. Identificouse unha persoa sospeitosa e nas súas roupas hai restos similares que pertencen ao pozo.

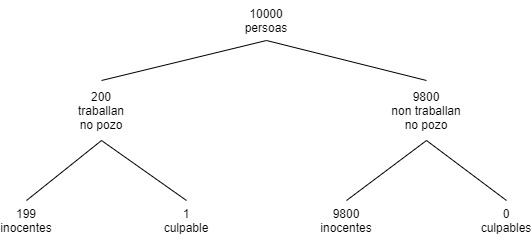
Chamamos E á evidencia, que son os restos minerais atopados, e I será a hipótese de que é inocente. Fíxese vostede que C e I son sucesos complementarios: unha e só unha é verdadeira.

Asumindo que é posible atopar restos similares nas roupas de todos os traballadores do pozo, podemos calcular a probabidade de atopar restos nunha persoa inocente: entre as 9999 inocentes da cidade, 199 traballan na mina.

   

Se o xuíz emprega este cálculo para supoñer que a probabilidade de que a persoa á que se lle encontraron os restos é inocente é de 0,02, estaría cometendo un erro na súa argumentación, pois estaría confundindo con P(I/E). Este dato, que é o que debería ter en conta, resúmese en que se poden atopar eses restos en 200 persoas, das cales 199 son inocentes. E por tanto:

   

Estas situacións aparecen cando a falacia se torna opaca debido a que hai unha probabilidade moi pequena (lembre, 1 posibilidade entre 73 millóns), senón resulta máis doado localizar o argumento falaz. A falacia da acusación aparece, dun xeito similar ao de Sally Clark, nun feixe de casos que transcenderon ao gran público. Pode vostede entreterse lendo sobre algún deles, coma o xuízo por asasinato a O.J. Simpson ou o caso «o pobo contra Collins»¹; en España pode atoparse a súa presenza no caso Sonia Carabantes².

Algunhas referencias:

• Carracedo, Ángel (2019). Matemáticas y ciencias forenses. Conferencia plenaria en las JAEM (Jornadas para el Aprendizaje y Enseñanza de las Matemáticas), A Coruña.

• Forte Deltell, Anabel (2022). ¿Cómo sobrevivir a la incertidumbre? Next Door, Pamplona.

• Gil Bellosta, Carlos J. “La falacia del fiscal (pero con frecuencias naturales). Recuperado o 27/08/2023 desta ligazón.

• Montes, Francisco (2003). Ley y probabilidad. Conferencia impartida no curso ‘Las matemáticas y sus aplicaciones en el mundo económico y social’ na Universidad Internacional Menéndez Pelayo, Santander. Recuperado o 27/08/2023 desta ligazón.

• Quintela del Río, Alejandro. “La falacia del fiscal”. Recuperado o 27/08/2023 desta ligazón.<https://bookdown.org/aquintela/>

• Yates, Kit (2019). The Maths of Life and Death. Why maths is (almost) everything. Quercus Editions, Londres.