Multiplicar e dividir fraccións

As operacións con fraccións parecen causar bastantes dificultades aos nosos escolares. No caso da suma e a resta o obstáculo semella máis computacional que comprensivo, pois son máis doadas de interpretar, pero o seu cálculo require reducir as fraccións a común denominador; é este último o paso que adoita atragoarse a unha cantidade nada desdeñosa de estudantes.

Porén, multiplicar e dividir fraccións adoita ofrecer menos problemas de cálculo, pero máis de entendemento. Quizais porque deseguida dominan as contas, os estudantes rapidamente dan por sabidas estas operacións e deixan a un lado a comprensión conceptual, o porqué de facérmolas coma as facemos. De aí que as vaiamos retomar nas liñas seguintes.

Como din Carvajal e Muñoz (2019), «as demostracións visuais non son estritamente demostracións formais, pero son imaxes belísimas relacionadas con propiedades ou teoremas que xeran ideas. Tamén son un recurso fantástico para o traballo intelectual matemático»¹. E así, un concepto ao que habitualmente damos un significado e uso eminentemente aritmético, numérico, nesta ocasión vai ser presentado dun xeito xeométrico buscando facilitar a comprensión destas ideas. Imos aló: toca multiplicar e dividir fraccións.

Partimos da multiplicación de números naturais, que imos representar graficamente mediante rectángulos. Si, imos traballar cun modelo baseado en áreas. Pare vostede un intre a lectura, e apréstese a coller unha folla cuadriculada para debuxar os rectángulos, a ben seguro que a visualización chegará con máis forza se me acompaña con lapis e papel e vai reproducindo o argumento segundo eu o vou presentando. O que imos facer é interpretar o produto de dous números da seguinte maneira: ao colocar unha das cantidades como a medida da base do rectángulo e a outra como a medida da súa altura, o resultado da multiplicación de ambas será a área dese rectángulo.

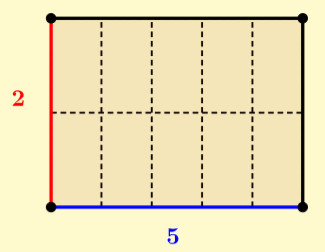
Na figura 1 visualízase o exemplo . Ao debuxar un rectángulo cunha anchura de 5 unidades e unha altura de 2 unidades, salta á vista que o rectángulo queda dividido en 10 celas. En conclusión, a multiplicación resulta ser .

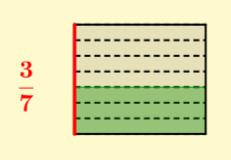
Esta mesma idea resulta de axuda na comprensión do produto de dúas fraccións. Novamente, representamos un dos números sobre a base dun rectángulo e o outro número sobre a altura. A área do rectángulo resultante indicará o valor da multiplicación de ambos os números. Para poder debuxar esta gráfica, primeiro debemos recordar como representar unha fracción graficamente: divídese a figura en tantas partes iguais como indique o denominador, e delas tómanse tantas como apunte o numerador (figura 2).

Unha vez que vostede recordou como representar fraccións nun rectángulo, xa pode enfrontar unha multiplicación coma por exemplo 2/5 · 3/7. A primeira fracción represéntase na base, a segunda na altura da figura 3.

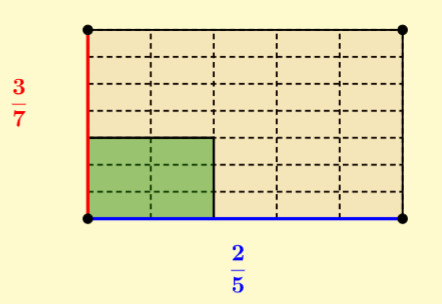
Horizontalmente o rectángulo queda dividido en 5 partes, verticalmente en 7 partes. En total, a figura inicial quedou escindida en 35 anacos, todos eles de igual tamaño. Dos 5 anacos horizontais eliximos 2, e dos 7 anacos verticais eliximos 3, o cal nos leva aos 6 anacos sombreados que se poden ver na figura 3. É dicir, a operación de multiplicación levou a dividir o rectángulo en 35 partes iguais, das cales quedamos con 6, ou o que é o mesmo, chegamos á fracción 6/35. Resumindo, xa sabemos como se multiplican dúas fraccións:

   

Entre as catro operacións básicas (adición, subtracción, multiplicación, división) para fraccións, seguramente a máis difícil de “dixerir” sexa a división, polo menos conceptualmente. Vostede non vai ler aquí a regra mnemónica que se adoita a repetir nas aulas, pois é ben abstrusa e non aporta ren á comprensión conceptual. Non, moito mellor faremos recaer de novo a explicación en imaxes, baseándonos unha vez máis na percepción visual.

Agora non imos botar man de rectángulos, pois se ben a partir dos seus lados a multiplicación proporciona a área do rectángulo, non sucede o mesmo coa división. É certo que poderiamos presentar a división mediante o modelos das áreas, claro que si, sen máis que tomala coma a operación inversa da multiplicación. É dicir, achegando outra vez un rectángulo do que coñecemos a área e unha das dimensións, pero non a outra, e queremos descubrir o valor desta. Funciona ben, aparece a división tal e como a coñecemos. Pero a min agora gustaríame presentar un argumento diferente para amosar unha variedade máis ampla de razoamentos. Quede vostede co que máis lle preste.

A división debemos entendela coma a razón entre dúas cantidades, ao calcular 3/4 ÷ 2/5 a pregunta que nos estamos a facer é, cantas veces cabe 2/5 dentro de 3/4? Intuitivamente, somos quen de afirmar que cabe máis de unha vez, xa que 2/5 é máis pequeno ca 3/4 (aquel é máis pequeno ca 0,5, mentres que 3/4 é máis grande). Porén, non é sinxelo a simple vista decidir exactamente cantas veces cabe, e o mesmo pasará sempre que o resultado non sexa un número enteiro, senón outra fracción.

Así as cousas, para representar graficamente estas razóns vai ser suficiente con empregar segmentos, que dividiremos en anacos con xeito. Lembre vostede, tantas partes iguais como indique o denominador, das cales marcamos tantas como indique o numerador.

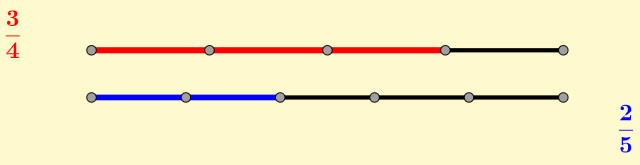
Na figura 4 pode verse que a división é difícil de avaliar directamente, pois na gráfica non queda nada claro cantas veces cabe 2/5 (o segmento azul, abaixo) en 3/4 (o segmento vermello, arriba). Precisamos dalgunha técnica grazas á cal quede patente a relación entre ambos os segmentos. E a chave van ser as fraccións equivalentes ás dadas que teñan un mesmo denominador. Si, a técnica coñecida como «reducir a común denominador», que tamén empregamos para a suma e resta de fraccións.

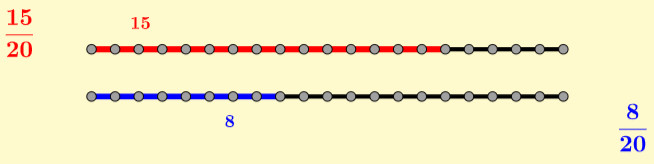
Amplificamos pois a fracción 2/5 por 4 para obter 8/20, e repetimos proceso con 3/4 por 5 para chegar a 15/20 (figura 5). Como agora ambos os segmentos están fragmentados en anacos de igual lonxitude, é máis doado realizar unha comparación entre eles. Neste caso podemos ver que 2/5 cabe en 3/4 do mesmo xeito que 8 cabe en 15, case dúas veces. O resultado non é exacto, e por iso era difícil de apreciar na figura 4, pero xa non queda dúbida de que a solución da división é 15/8. Resumindo, sabemos tamén como se dividen dúas fraccións:

   

E até aquí chegamos con esta revisión de como multiplicar e dividir fraccións, que era o obxectivo para a entrada de hoxe.

Algunhas referencias:

• Carvajal Sánchez, Ana e Muñoz Casado, José Luis (2019). Demostraciones visuales en matemáticas. Los Libros de la Catarata, Madrid.

• Sawyer, W.W. (2007). Mathematician’s delight. Dover, New York.