O paradoxo de Allais

A teoría da decisión é unha área do saber que se ocupa da análise na toma de decisións, do estudo do comportamento e o seguimento de estratexias perante situacións que requiran tomar algunha resolución. Os especialistas nesta materia tratan de examinar como unha persoa elixe unha acción concreta entre o conxunto de accións posibles que se lle presentan, partindo da base de que busca o mellor resultado posible.

Un interesante problema que se encadra na teoría da decisión é o paradoxo de Allais, presentado no ano 1953 por Maurice Allais (1911-2010). O paradoxo supón unha contradición á teoría da utilidade esperada, que non é máis ca un modelo que supón que, en decisión tomadas con incerteza, a elección preferida polos individuos será aquela que conte cunha utilidade esperada máis alta.

Expliquemos o exemplo típico de situación na que agroma o paradoxo de Allais, consistente na combinación de dous experimentos de similar cariz nos cales a un individuo se lle ofrecen dúas opcións. Toman forma de lotería, con dúas opcións con distintos premios, das que cales se debe elixir unha.

O primeiro experimento e tal que así:

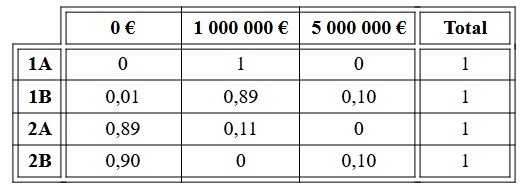
• 1A → 1 millón de euros, con probabilidade 1.

• 1B → 1 millón de euros con probabilidade 0,89; 5 millóns de euros con probabilidade 0,10; sen premio con probabilidade 0,01.

O segundo experimento é destoutro xeito:

• 2A → 1 millón de euros con probabilidade 0,11; sen premio con probabilidade 0,89.

• 2B → 5 millóns de euros con probabilidade 0,10; sen premio con probabilidade 0,90.

Antes de proceder co estudo desta situación, e de que eu lle explique por que a inclúo no capítulo dos paradoxos, dedique vostede uns intres a tomar a súa propia decisión. Que elixe? Primeiro pense se quedaría con 1A ou con 1B, e a continuación decida se opta por 2A ou por 2B. Unha vez determinada a súa preferencia, apunte a dobre escolla e prosiga coa lectura.

Agora, o primeiro que imos comprobar á vista dos datos é que todas as opcións sumen probabilidade 1 ( que sumen o 100 %, se prefire traballar con tantos por cento); son unhas contas moi doadas que se recollen na táboa 1.

O seguinte paso que vou dar na análise destes experimentos será o cálculo do retorno esperado de elixirmos cada unha das opcións, que se recolle na táboa 2.

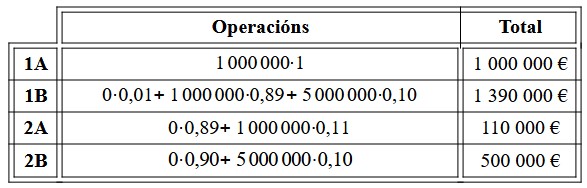
Observando os números propostos nos experimentos e os cálculos feitos, penso que hai dous posibles razoamentos para realizar as escollas, en función do que priorice o individuo que xoga a estas loterías. Aquelas persoas que queiran maximizar os beneficios, sen importarlle se o risco de non gañar nada é maior ou menor, optarán polas opcións 1B e 2B, que ofrecen un retorno esperado máis elevado. Por contra, aquelas que mostren maior aversión ao risco escollerán 1A e 2A, pois en ambas é menor a probabilidade de non gañar ningún premio. Vostede cal elixiu? Seguiu un argumento semellante ao meu para desequilibrar a balanza entre as distintas opcións?

Eses dous resultados aos que cheguei seguen a teoría da utilidade esperada, resúmense en que un individuo que prefire un retorno máis seguro aínda que sexa máis baixo, elixe as opcións A, mentres que outro individuo que se inclina por retornos máis alto a pesar de teren maior inseguridade, quedaría coas alternativas B.

E despois de todo isto, onde está o paradoxo? Hai dúas combinacións lóxicas e perfectamente compatibles, que dependen da personalidade de quen realice a escolla, pois cada quen é un mundo e non todas as persoas temos as mesmas preferencias, pero en todo ambas as resolucións son coherentes. Pois resulta que a inconsistencia xorde coa posta en práctica dos experimentos, xa que varios estudos¹ tiraron resultados nos que a resposta máis frecuente -incluso maioritaria- era a escolla das opcións 1A e 2B. E iso é o paradoxal, dado que esa decisión resulta dificilmente defendible.

Velaí a incongruencia coa teoría da utilidade esperada: moitas persoas pasaron de elixir o retorno máis seguro e baixo no primeiro experimento a escoller o retorno máis inseguro e alto no segundo, sen que aparentemente nada xustifique tal cambio.

Cal pode ser a explicación a esta contradición? Unha posibilidade que a clarificaría é que non haxa tal contradición porque a teoría da utilidade esperada non sexa válida en todas as ocasións; isto acabaría co paradoxo de Allais e con outras discrepancias existentes. Ou ben podería xustificarse pola falta de racionalidade nas escollas dun amplo espectro da poboación, relacionada co anumerismo, a incomprensión do cálculo de probabilidades ou a inexistencia dunha análise lóxica. Tamén podería ocorrer que o valor que unha persoa asigna a cada consecuencia non coincida coa súa probabilidade real, o que pode darse cando se avalían sucesos de escasa probabilidade – coma o 1% extra que ten o quedar sen premio nas opcións B respecto das A- nunha medida maior da que merecerían.

Uns cantos estudosos realizaron investigacións para intentar entender o que ocorre ante este tipo de escenarios hipotéticos. En 1979, Daniel Kahneman (n. 1934, foi premio Nobel de Economía no ano 2002) e Amos Tversky (1937-1996) realizaron varios experimentos tras os que concluíron que os individuos tenden a sobreestimar sucesos case seguros respecto daqueles que son simplemente probables; á utilidade escápaselle certo patrón psicolóxico que os humanos levamos máis alá da pura racionalidade. De feito, parece haber consenso no feito de que en situacións de incerteza non buscamos o mesmo tipo de resultados se as decisións pesan sobre ganancias ou sobre perdas.

A miña conclusión está clara: a teoría da decisión non é para nada tan doada como poida parecer a priori, e as decisións -supostamente- racionais da xente non sempre atopan explicacións razoables. De feito, nesa liña existe un concepto chamado ‘efecto marco’, proposto polo propio Kahneman, que vén ser un nesgo polo cal as preferencias da xente ante un problema dos que se encadran na teoría da decisión depende da forma na cal se presenta o devandito problema. Vamos, que cambiar o papel co que se envolve o paquete sen alterar este nin o máis mínimo, provoca reaccións diferentes no receptor. E son moitas as evidencias empíricas ao respecto. Curioso, non si?

Algunhas referencias:

• Allais, Maurice (1953). Le Comportement de l’Homme Rationel devant le Risque, Critique des Postulates et Axiomes de l’École Americaine. Econometrica, volume 21, pp. 503-546.

• Gallardo Ku, José D. (2018) .Notas en teoría de la incertidumbre. Fondo editorial, Lima.

• Kahneman, Daniel e Tversky, Amos (1979). Prospect Theory: An Analysis of Decision under Risk. Econometrica, volume 47(2), pp. 263-292.

• Machina, Mark (1987). Choice Under Uncertainty: Problems Solved and Unsolved. Economic Perspectives, volume 1, número 1, pp. 121-154.

• Morrison, Donald G. (1967). On the Consistency of Preferences in Allais’ Paradox. Behavioral Science, volume 12, pp. 373-383.

• Raiffa, Howard (1968). Decision Analysis: Introductory Lectures on Choice Under Uncertainty. Addinson-Wesley, Reading (Massachusetts, EUA).

• Slovic, Paul e Tversky, Amos (1974).Who Accepts Savage’s Axiom? Behavioral Science, volume 19, pp. 368-373.