Hai unhas décadas adoitaba tomarse a expresión ‘ciencias exactas’ practicamente como sinónimo de ‘matemáticas’, pero hai xa tempo que ningunha disciplina reivindica para si mesma tal condición de exactitude. Si perdura, non obstante, certa tendencia a conferir ás matemáticas un elevado grao de precisión, cousa que sucede en gran medida por parte de persoas alleas a elas. As entendidas saben ben que nalgunhas ocasións se dá esa exactitude, e noutras non.
En resumidas contas, nas matemáticas non sempre existe unha solución única nin un só razoamento válido cando se trata de resolver un problema. Xa contei nos Bocados Matemáticos (2022, Edicións Xerais) como o teorema de Pitágoras ten o récord Guinness para o teorema con máis demostracións diferentes -cóntanse por centos-.
O paradoxo do que vou falar a continuación sitúase neste contexto: imos partir dunha situación que nos levará a resultados distintos segundo cal sexa a liña de pensamento que sigamos. Mesmo punto de partida, diferentes puntos de chegada. Vaise enmarcar no eido da probabilidade, e a ben seguro que vostede xa sabe o contraintuitiva que pode chegar a ser esa rama das matemáticas, con que facilidade agroman nela contradicións, absurdos e sensentidos.
Chámase paradoxo de Bertrand, e si, efectivamente, debémosllo a Joseph Bertrand (1822 – 1900), quen o introduciu na súa obra Calcul des Probabilités no ano 1888. Vaia vostede facendo quecementos cos músculos faciais, que estou convencido que o que lle vou contar o deixará coa boca aberta e non quero que iso lle produza ningunha escordadura.
Comezamos por unha figura sinxela como é un triángulo equilátero. Recorde o que iso significa: ten os seus tres lados iguais, e tamén ten os seus tres ángulos iguais (todos miden 60º). Este é un bo momento para facer unha parada na lectura e coller papel e lapis; siga as explicacións ao tempo que debuxa. Comece co triángulo, dá igual o tamaño pero debe ser equilátero.
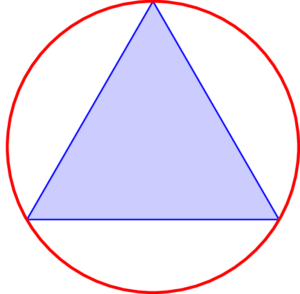
A continuación debuxamos a circunferencia circunscrita ao triángulo (aquela que pasa polos seus tres vértices). Pode vela na figura 1. E iso xa nos coloca na liña de saída. O problema que quería achegar é o seguinte: cal é a probabilidade de que unha corda escollida ao azar sexa máis longa que o lado do triángulo? Por se non o lembra, unha corda é calquera segmento recto que una dous puntos da circunferencia.
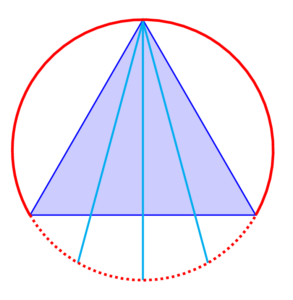
Un posible razoamento consistiría en buscar puntos finais aleatorios. Para iso fíxase un punto calquera, por exemplo o vértice superior do triángulo, e logo pénsase en todas as cordas que se poden formar cun extremo nel (son infinitas, habería unha por cada punto da circunferencia salvo o propio vértice, de aí que dixese antes que buscaría os puntos finais). Deste xeito as cordas son máis longas que o lado do triángulo se e só se o segmento queda dentro do ángulo que se forma no vértice. Tal e como se ve na figura 2 o triángulo divide a circunferencia en tres arcos de 120º, e as cordas máis longas ocuparían xusto un dos tres arcos. A conclusión inmediata sería que a probabilidade buscada é 1/3.
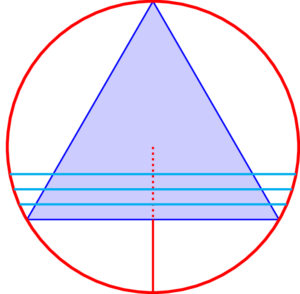
Convenceuse? Si? Non? Pois téñolle outro razoamento, xa verá. Un que usa o raio da circunferencia. Por comodidade vou tomar o raio perpendicular ao lado horizontal do triángulo. Tómase un punto aleatorio dese raio (ten infinitos, como calquera segmento) e constrúese a corda perpendicular ao raio que pasa por ese punto. A figura 3 permite visualizar o que estou dicindo. As cordas serán máis longas que o lado se o punto tomado sobre o raio está entre o centro do triángulo e o lado, e máis curtas se o punto está entre o lado e a circunferencia. Pero como o lado do triángulo divide ao raio xusto pola metade, entón a conclusión é que a probabilidade buscada é 1/2.
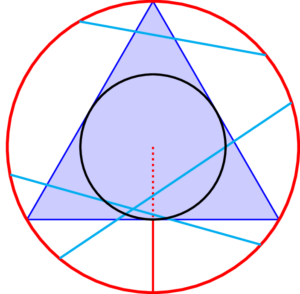
Pero, como? Un medio? Pero non era un terzo? En que quedamos? U-las ciencias exactas? Pois agarre a cabeza antes de que comece a abanear, que lle traio outro razoamento. Aquí, en exclusiva e para vostede. Unha corda é máis longa que o lado do triángulo se o seu punto medio cae dentro dun círculo inscrito dentro do triángulo. Vexa a figura 4 para orientarse. Este círculo interior ten un raio que é a metade do raio do círculo exterior e, polo tanto, unha área que é a cuarta parte da área do círculo exterior. En conclusión, a probabilidade buscada ten que ser 1/4.
Isto xa é o non vai máis. Mesma situación, e segundo o razoamento empregado chegouse a tres probabilidades diferentes: un medio, un terzo e un cuarto. Repase vostede os argumentos seguidos, repase, e se atopa algunha falla avise. Pero gardo outro as na manga: non quero aburrilo estendéndome máis, pero resulta que existen aínda máis procedementos que levan a aínda máis resultados distintos. Quedamos con estes tres porque son os que o propio Bertrand presentou inicialmente.
Entón, cal é o sentido de todo isto? Como é posible que se obteñan distintas probabilidades? Iso non debería ser así, non? Vostede ha estar a pensar que teriamos que ser quen de decidir cal é o argumento correcto, e por tanto a probabilidade buscada. Vostede ha estar a pensar que eu no seguinte parágrafo lle vou desvelar algún erro, ou presentar outro razoamento que socave os alicerces dos tres anteriores. Vostede quere exactitude.
Tense escrito bastante sobre este problema, aínda que boa parte dos autores non expresan unha preferencia definida entre as distintas opcións que antes explicaba. Edwin Jaynes (1922 – 1998) publicou en 1973 que a medida da probabilidade debe estar dotada de invariancias rotacionais, de escala e de translación. Dous observadores separados a unha distancia deberían chegar a conclusións iguais, o mesmo que dous observadores que o fan dende distintos ángulos. Aplicando eses principios, Jaynes colixía que no problema que nos ocupa a probabilidade debe ser 1/2, afirmando tamén que esa solución se verificara experimentalmente.
Porque en realidade, que é o que se esconde detrás deste paradoxo? Pois curiosamente, o quid da cuestión reside na idea mesma de ‘azar’. Resulta que a probabilidade non está ben definida se o método que produce a variable aleatoria a estudo non está claramente definido. Dito doutro xeito, o efecto paradoxal apareceu pola forma en que tomamos puntos ou cordas “aleatorias”. Ese termo non está ben concretado, hai moitas maneiras de facelo e para escapar do paradoxo hai que precisalo con anterioridade. Vamos, que o erro non reside en ningún dos razoamentos anteriores, senón na propia pregunta inicial, xa que falla ao non especificar de que maneira a corda se elixe aleatoriamente. Isto é o que fixo Jaynes: dotar á probabilidade das propiedades que ten que cumprir antes de examinar o problema, e xusto iso é o que consegue levalo a unha única solución.
Ben sei que non é a resposta que agardaba, pero sérveme para explicarlle tamén que aos propios matemáticos lles custou moito entender axeitadamente a probabilidade, e non foi até xa entrado o século XX (na década dos trinta) cando Andrei Kolmogorov (1903 – 1987) estableceu a definición axiomática da probabilidade que hoxe coñecemos e empregamos. Que se estuda nos institutos deste país. De feito, se revisamos o currículo de secundaria da materia de Matemáticas, é un dos poucos contidos que aparece que sexa do século XX (e así de memoria, diría que ningún do XXI). A meirande parte deles desenvolvéronse con anterioridade ao 1900.
Algunhas referencias:
-
Chamizo, Fernando. Tres joyas matemáticas de Joseph Bertrand.
<https://elpais.com/ciencia/cafe-y-teoremas/2023-03-07/tres-joyas-matematicas-de-joseph-bertrand.html>
-
Clark, Michael (2012). Paradoxes from A to Z. Routledge, Londres.
-
Jaynes, Edwin T. (1973). The Well-Posed Problem. Revista Foundations of Physics, 3, pp 477-493.
-
Morales, Miguel Ángel. La paradoja de Bertrand: triángulos, circunferencias y probabilidad.
<https://elpais.com/elpais/2016/10/11/el_aleph/1476221762_063573.html>