Números construíbles con regra e compás

Noutros apartados xa falamos do apaixonante mundo das construcións con regra e compás. Das normas que rexen as devanditas construcións. Dos tres problemas clásicos: a cuadratura do círculo, a duplicación do cubo e a trisección do ángulo. Dos polígonos regulares que se poden construír con esas dúas ferramentas, e para cales tal cousa non é posible.

Así que agora toca falar de números, pero non de operacións nin das súas propiedades. Imos ver cales son os números construíbles con regra e compás, suxeitos ás normas que xa mencionamos. Que, no fondo, é a idea chave na que se basean as demostracións da imposibilidade dos problemas clásicos. A tales números darémoslle o nome de ‘números construíbles xeometricamente’.

En todo momento partiremos dunha medida dada que nos sirva como base. Recordemos que a regra que se usa neste tipo de construcións é non graduada, polo que non podemos usala para tomar medidas. Por tanto, o que facemos é coller un segmento calquera e empregalo como padrón, é dicir, asignámoslle 1 unidade de lonxitude.

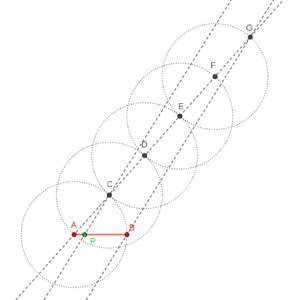
A partir dese segmento unidade AB resulta moi doado construír todos os números enteiros. Primeiro, usamos a regra para estender o segmento en ambos os sentidos. Pinchamos o compás no extremo B do segmento e fixamos a súa abertura igual a AB, que é o noso segmento unidade. Ao facermos traballar o compás, o punto C no que corta á recta estendida marcará 2 unidades de lonxitude, AC. Pinchando o compás en C e reiterando os pasos, constrúense o resto de números naturais: 3, 4, 5 etc. Se repetimos todo isto, pero pinchando en A e construíndo os puntos cara a esquerda, obteremos tamén os números negativo: -1, -2, -3 etc. A construción queda tal e como se ve na figura 1, todos os números enteiros son construíbles xeometricamente.

Continuando cos conxuntos numéricos, o seguinte é o dos números racionais. As fraccións. Imos comezar por construír as fraccións que teñen un 1 no numerador, aquelas que son da forma $\frac{1}{q}$ .

Vexamos o procedemento cun exemplo concreto coma $\frac{1}{5}$ . Partimos novamente do segmento unidade AB, de lonxitude 1. O procedemento completo está recollido na figura 2. Trazamos coa regra unha recta auxiliar que pase por A, dá un pouco igual por onde, pero que nos resulte cómoda. Pinchamos co compás no extremo A e fixamos a abertura co segmento AB. Marcamos o punto de corte coa recta auxiliar, C. Repetimos o proceso para marcar os puntos D, E, F, G, collendo sempre unha amplitude da mesma lonxitude. En total son 5 puntos, xa que queremos achar un quinto.

O paso seguinte consiste en unir, coa regra, o punto inicial A co último construído, neste caso G. A continuación, trázase unha paralela¹ a esta última recta, que pase polo punto C. O punto de corte, P, desta paralela co segmento inicial AB, determina unha lonxitude $\frac{1}{5}$ respecto de A.

Figura 2. Construíndo 1/5 xeometricamente.

Este método é a aplicación dun resultado que se estuda nas aulas de matemáticas da educación secundaria: nin máis nin menos que o teorema de Tales. O que nos permite asegurar este teorema é que, dadas dúas rectas secantes (o segmento inicial e a recta auxiliar), se trazamos rectas paralelas que as corten, os segmentos que determinan son proporcionais. Traducimos: como por construción o segmento AC é a quinta parte de AG, entón o segmento AP tamén é a quinta parte de AB. Podemos escribir isto simbolicamente:

$\dfrac{AC}{AG}=\dfrac{AP}{AB} \quad \Rightarrow \quad \dfrac{1}{5}=\dfrac{AP}{1} \quad \Rightarrow \quad AP=\dfrac{1}{5}$

Este método que usamos co denominador 5 é perfectamente xeneralizable para calquera denominador q, e por tanto é o que nos permite construír xeometricamente calquera fracción da forma $\frac{1}{q}$ . Como é obvio, non todas as fraccións teñen esa forma, pero calquera outra fracción será da forma $\frac{p}{q}$ , pero ese caso consiste simplemente en construír primeiro $\frac{1}{q}$ , e xusto a continuación prolongar coa regra o segmento AB e marcar p puntos con medida AP, tal e como vimos ao construír os enteiros. E listo, resulta que podemos construír xeometricamente todos os números racionais.

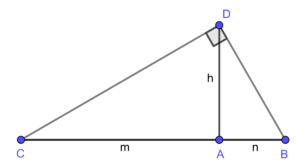
Pero isto non acaba aquí. Imos ver como construír a raíz cadrada $\sqrt{a}$ dun número natural a. Botaremos man dun novo resultado que se adoita traballar nas aulas de secundaria: o teorema da altura². Imos recordalo, por se acaso a vostede xa lle esqueceu (figura 3). Nun triángulo rectángulo, se trazamos a altura h correspondente ao ángulo recto, o cadrado desta altura é igual ao produto dos dous segmentos nos que queda dividida a hipotenusa, m e n. Simbolicamente tense que $h^2=m\cdot n$ ³.

Figura 3. Teorema da altura. — Figura 3. Teorema da altura: $h^2=m\cdot n$ .

Figura 3. Teorema da altura: $h^2=m\cdot n$ .

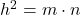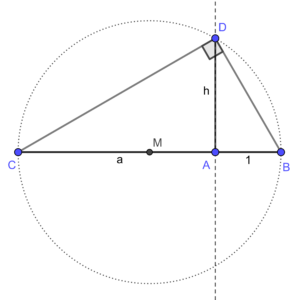
Unha vez recordado isto, imos coa construción. Vaia fixándose na figura 4 para seguila. Comezamos co segmento unidade AB, e xa sabemos construír o número natural a (foi o primeiro que fixemos), que na figura é o segmento CA. Construímos despois a perpendicular que pasa por A⁴. Construímos tamén M, o punto medio entre C e B⁵, e pinchamos nel o compás para trazar a circunferencia que pasa por B e C. E xa estaría, marcamos o punto D onde se cortan a perpendicular e a circunferencia, e resulta que o triángulo BCD é rectángulo, porque ao estar inscrito na circunferencia e ser o seu lado BC un diámetro desta, está garantido que o ángulo que se xera en D é recto.

Figura 4. Construíndo raíces. — Figura 4. Construíndo $\sqrt{a}$ .

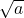Dixen triángulo rectángulo? Dixen, si, e por tanto podemos aplicar o teorema da altura para despexar e obter o valor desexado $\sqrt{a}$ :

$h^2=a\cdot 1 \quad \Rightarrow \quad h=\sqrt{a}$

Xa somos quen de construír, pois, os números enteiros, as fraccións e as raíces cadradas dun número natural. Non nos imos estender nestas páxinas, pero é posible demostrar que, unha vez construídos xeometricamente dous números a, b, tamén se poden construír $a\pm b, a\cdot b, \frac{a}{b}$ , o cal permite construír con regra e compás números tales coma $-4+\frac{2}{7},1+\sqrt{2}$ ou incluso outros aparentemente tan enrevesados coma $\frac{\sqrt{-2+\sqrt{5}}}{\sqrt{1+\sqrt{2+\sqrt{3}}}}$ .

Resumindo: os números construíbles con regra e compás son todos aqueles que se obteñen dos números enteiros mediante suma, resta, multiplicación, división e extracción de raíces cadradas. Pero, tal e como falaramos no apartado Os tres problemas clásicos da regra e o compás, non é posible conseguilo para o resto de números, esquézase de construír así $\sqrt[3]{2}$ ou $\pi$ .

Algunhas referencias:

Blog Compás e regra. <https://compaseregra.blogspot.com/>.

Sultan, Alan e Alice F. Artzt (2011). The mathematics that every secondary school math teacher needs to know. Routledge, Nova York.

1Trazar unha recta paralela a outra recta dada, pasando por un punto exterior a esta última, é unha construción que se pode facer con regra e compás. Como non é obxectivo deste apartado, e para non complicar a lectura destas páxinas, déixolle unha ligazón onde pode ver como facelo: <https://compaseregra.blogspot.com/search/label/paralela>.

2Tamén se pode basear a construción de no teorema de Pitágoras, pero a min gústame máis facelo co teorema da altura.

3Realmente, o teorema da altura non é máis que aplicar a semellanza existente entre os triángulos ACD e ADB.

4Para o trazado da recta perpendicular por un punto exterior a unha recta dada, déixolle outra vez unha ligazón para que vexa distintas formas de facelo: <https://compaseregra.blogspot.com/search/label/perpendicular>.

5De novo, unha ligazón para amosar como achar o punto medio: <https://compaseregra.blogspot.com/search?q=punto+medio>.

Deixa un comentario Cancelar a resposta