Polígonos regulares con regra e compás

por

Xa se falou aquí da xeometría clásica das construcións con regra e compás e da imposibilidade dentro dela da realización dos tres problemas clásicos: a duplicación do cubo, a trisección do ángulo e a cuadratura do círculo. Imos retomar o tema para falarmos nesta ocasión de polígonos regulares construíbles con regra e compás.

Cómpre lembrar que un polígono regular é todo polígono no cal os lados e os ángulos interiores son iguais entre sí. As dúas condicións son necesarias e para entendelo pense vostede que un rombo non é regular (ten todos os lados iguais, pero non os ángulos interiores) e un rectángulo tampouco o é (posúe todos os ángulos interiores iguais, mais non os lados).

Vou formular o problema buscando construír os polígonos regulares coas normas clásicas da regra e o compás a partir dalgún dato inicial, como poida ser o círculo circunscrito ou un dos sus lados. Neste último caso resultaría indiferente qué lado se toma dado que acabamos de dicir que son todos iguais. Unha pregunta agroma rapidamente: «é posible construír dese xeito calquera polígono regular?».

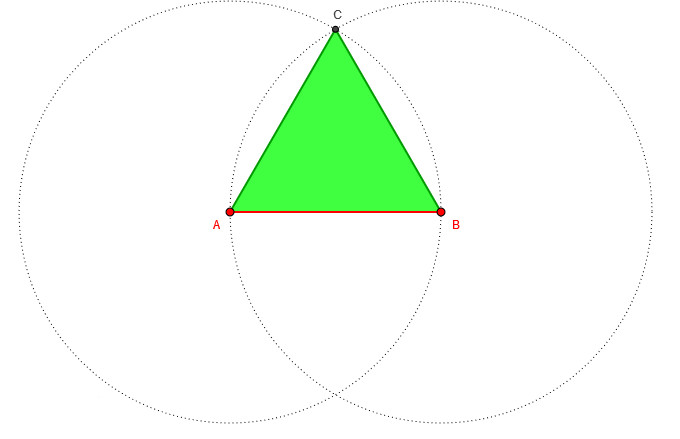
É moi doado construír o triángulo regular -habitualmente chamado triángulo equilátero- a partir dun lado, basta con trazar dúas circunferencias, cada unha centrada nun dos extremos do lado de partida e pasando polo outro dos extremos. Únese o punto de intersección das circunferencias cos extremos do lado, e listo (figura 1).

Polígonos regulares con regra e compás. O triángulo
Figura 1. Construción do triángulo equilátero regular a partir dun lado dado.

Cun chisco máis de esforzo, pero sendo tamén unha construción sinxeliña1 pode obterse o polígono regular de catro lados -o cadrado-. E igualmente é posible construír o pentágono regular (de 5 lados) e o hexágono regular (de 6 lados)… conséguese con todos ou non?

Pois ben, a resposta é que hai polígonos regulares que NON se poden construír coas normas clásicas da regra e o compás. Deles, o heptágono regular (de 7 lados) é o que ten menor número de lados. E o eneágono (de 9 lados) ou o endecágono (de 11 lados) regulares tampouco o son. En matemáticas sempre se anda a buscar teoremas que xeralicen os problemas nos que se anda a traballar, e neste caso temos o seguinte:

Un polígono regular de n lados é construíble coas normas clásicas da regra e o compás se e só se n pode descompoñerse en factores primos da forma:

    \[n=2^r \cdot p_1 \cdot \cdots \cdot p_k\]

, sendo r\geq 0 e os factores primos p_i primos de Fermat distintos entre si.

Lembremos que un número primo é un número natural maior que 1 que só ten dous divisores, el mesmo e mais o 1. Iso dos primos de Fermat refírese simplemente aos números primos que son da forma 2^{2^n}+1. Na actualidade os únicos primos de Fermat coñecidos son 3, 5, 17, 257, 65 537, xa que:

2^{2^0}+1 = 2 + 1 = 3

2^{2^1}+1 = 2^2 + 1 = 5

2^{2^2} +1 = 2^4 +1 =17

2^{2^3}+1 = 2^8+1 = 257

2^{2^4}+1 = 2^{16}+1 = 65\ 537

Este dos polígonos regulares con regra e compás é un tema apaixoante, sobre o cal o propio Pierre de Fermat (1601 – 1665, figura 2) conxecturou que todos os números desa forma sería primos. Se vostede ten gana de entreterse un bo anaco, pode facer algúns cálculos co seguinte valor de n, pero xa lle adianto que o fixo Leonhard Euler (1707 – 1783) por nós, demostrando en 1732 que se n = 5 o número obtido é composto, nada máis e nada menos que 2^{2^5}+1 = 2^{32}+1 = 4\ 294\ 967\ 297 = 641\cdot 6\ 700\ 417. Tal e como dicía antes, hoxe en día só se sabe deses 5 primos de Fermat, pero o noso descoñecemento é tan grande que non temos nin idea de se efectivamente só hai eses cinco… ou se incluso pode haber infinitos.

Pierre de Fermat
Figura 2. Pierre de Fermat, máis famoso polo Último Teorema de Fermat que pola conxectura do primos de Fermat. Fonte: Wikimedia Commons.

 

Xa estamos en condicións de retomar o teorema enunciado mais arriba, que nos permite concluír que os polígonos regulares construíbles con regra e compás son aqueles que teñen un número de lados que sexa unha potencia de 2, un primo de Fermat (3, 5, 17, 257, 65 537) ou unha multiplicación entre eles. E imos apoiarnos no teorema para mostrar por que o heptágono regular e o eneágono regular non son construíbles, pero os demais polígonos regulares até 10 lados si o son:

3=2^{2^0}+1 4=2^2 5=2^{2^1}+1 6=2\cdot \left( 2^{2^0}+1 \right)
7\neq 2^{2^n}+1\ \forall n 8=2^3 9=3^2\neq 2^{2^n}+1\ \forall n 10=2\cdot \left( 2^{2^1}+1 \right)

Este resultado debémosllo aos esforzos de Carl Friedrich Gauss (1777 – 1855) e de Pierre Wantzel (1814 – 1848). O primeiro deles demostrou a suficiencia da proposición, mentres que o segundo probou a necesidade da mesma. Necesidade e suficiencia son termos utilizados en lóxica para describir unha relación entre dúas sentencias, e baste un exemplo para entedelos: estar dando un paseo por Pontevedra é condición suficiente para asegurar que se está en Galicia, pero non é necesario. No caso que nos ocupa, que o teorema inclúa tanto a necesidade coma a suficiencia significa que se o polígono regular é construíble con regra e compás, entón obrigatoriamente a descomposición de n ten que ser daquela forma, e tamén que se n se descompón así, obrigatoriamente o polígono regular ten que ser construíble. Podemos percorrer a estrada en ambos os sentidos.

Gauss publicou a súa demostración no libro Disquisitiones arithmeticae, escrito en 1798. Proporcionou a proba de que o heptadecágono regular (de 17 lados) é construíble, pero non propuxo unha construción propiamente dita. Non deixaba lugar a dúbida: podía facerse… só que el non dicía cómo. Algo non tan estraño en matemáticas, ser quen de demostrar un teorema de existencia pero non de proporcionar o método que nos leve a bo porto.

17=2^{2^2}+1, e por tanto a construción do heptadecágono era posible, só que houbo que esperar máis tempo por ela. Foi Johannes Erchinger (1788 – 1829) quen propuxo unha por primeira vez, en 1825, uns cantos anos máis tarde do resultado de Gauss que aseguraba a súa existencia.

Polígonos regulares con regra e compás. O heptadecágono.
Figura 3. Así queda o heptadecágono regular tras ser construído partindo do círculo circunscrito co método que debemos a Herbert William Richmond (ano 1893).

Por último só me queda engadir que no caso de non ser o polígono regular construíble, existen métodos para coa regra e o compás obter aproximacións do polígono. Algunhas son bastante boas, moi próximas ao polígono exacto; por exemplo xa Herón de Alexandría (10 – 70) empregaba unha aproximación para o heptágono regular na cal o ángulo central era de 51,318…º no canto dos 51,428571…º que mide no heptágono regular exacto.

Algunhas referencias:

4 comentarios en “Polígonos regulares con regra e compás”

  2. Ola Ignacio. Se non me trabuco, mirando por enriba creo que a construción que enlazas é a mesma que fixen eu en https://compaseregra.blogspot.com/2014/12/17-agono-regular-en-un-circulo.html.

    A diferenza principal é que eu incluín todos os pasos con regra e compás (nesas construcións non uso os comandos de GeoGebra para recta perpendicular ou para ángulo bisector).

    Nese caso, debémoslla a Herbert William Richmond (ano 1893).

    Por certo, xa gardei en Marcadores a nova dirección da túa web. Ao final tocou mudanza…

    Un saúdo, Paulo.

    Responder

  3. Creo que la construcción la tomé de una entrada del blog de Gaussianos de 12/12/2011 (https://www.gaussianos.com/construccion-del-heptadecagono-con-geogebra/), y no es la misma que la que enlazas. Por cierto que no lo cito en al applet y debería. Ahora que he redescubierto de donde la saqué, la pondré. En Gaussianos dicen que es la de Johannes Erchinger.

    Por cierto que en este video https://www.youtube.com/watch?v=FIJm5rbGuwo se la atribuyen al propio Gauss, lo que parece claro que no es cierto. No es la unica exactitud que contiene: al final afirma que solo pueden construirse los que tienen un número de lados igual a una potencia de 2 o a un primo de Fermat, contradiciendose incluso con lo que dice al inicio del video, ya sin contar los que tienen, no repetidos, más de un primo de Fermat.

    Saludos,

    Ignacio.

    Responder

Deixa un comentario