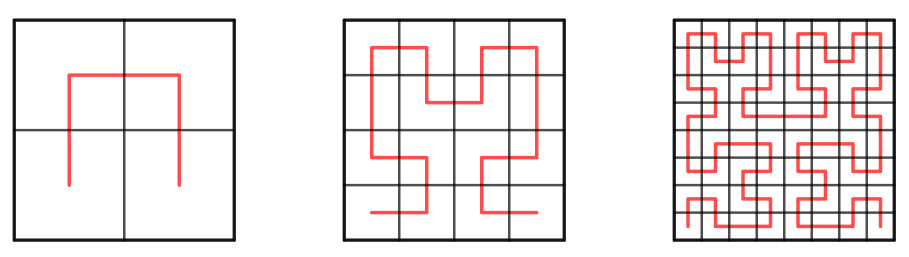
A curva de Hilbert

A curva de Hilbert é unha construción xeométrica moi doada de elaborar e que conta cunhas propiedades ben curiosas. Para coñecela, o primeiro que se debe facer é definila, e iso faise mediante un algoritmo recursivo (vostede pode intentar debuxala con lapis e papel seguindo a definición, ou pode optar por observar directamente a figura 1, onde aparecen as primeiras etapas do proceso):

Para comezar divídese o cadrado unidade (o que ten lado de 1 unidade) en catro cadrados iguais, e únense os centros destes últimos mediante segementos, empezando polo inferior esquerdo e rematando polo inferior dereito.

Na segunda etapa cada cadrado do paso anterior subdivídese en catro novos cadrados. Realízanse catro copias da primeira figura, pero reducidas ao 50%. Xíranse as dúas inferiores, unha cara cada lado, e volven unirse os centros dos cadrados.

O proceso pode repetirse indefinidamente repetindo os mesmos pasos, e o resultado que se obtén no límite é unha fermosa e interesante curva continua¹, bautizada na honra do matemático que foi o primeiro en describir este obxecto: David Hilbert (1862 – 1943), aló polo 1891, seguindo outro exemplo similar que un ano antes definira Giuseppe Peano (1858 – 1932).

É esta pois unha curva poligonal² tal que a súa curva límite ten unha lonxitude infinita, xa que se pode comprobar que se é a n-ésima iteración, a distancia total que percorre a curva é e a dita expresión medra exponencialmente ao aumentar n.

Pero a pregunta que se pode formular calquera é: «cal é a dimensión deste obxecto xeométrico?» Por un lado é unha curva, e debería por tanto ser unidimensional; por outro lado ocorre que recobre o plano no cal está definida, enchendo completamente o cadrado inicial segundo se vai reiterando o proceso, e por conseguinte tería que ser bidimensional.

Resulta que a curva de Hilbert -e moitas outras de similar atractivo coma a curva de Koch, ou tamén conxuntos coma o de Julia- pertence á xeometría fractal, unha rama das matemáticas que non existía até a pasada década dos setenta cando Benoît Mandelbrot (1924 – 2010) a introduciu. Foi el mesmo quen acuñou o termo ‘fractal’ para referirse ao grao de rugosidade dunha figura, termo que provén do latín ‘fractus’ e significa ‘fragmentado, roto’.

O que acontece é que nesta xeometría agroma un novo concepto de dimensión, que xeraliza o de dimensión ordinaria para tratar de determinar cómo un patrón (fractal) cambia coa escala na cal se mide. Existen diferentes formas de definir esta dimensión fractal, con frecuencia equivalentes, e a súa característica máis destacada é que poden ser fraccionarias. Non, non me trabuquei, dixen fraccionaria, e por exemplo a dimensión fractal para o triángulo de Sierpinski (pode buscar vostede cómo se constrúe e qué imaxes se obteñen, asegúrolle que merece a pena) é 1,585.

No exemplo que vimos de expor neste apartado, o da curva de Hilbert, a dimensión fractal vén ser 2. Todas as curvas que enchen o plano (coma tamén a de Peano á que nos referimos ao principio) teñen esa mesma dimensión fractal, que coinciden coa do espacio que enchen; un cadrado unidade ten dimensión 2 en calquera definición de dimensión que se dé.

Parece mentira que se trate dunha especialidade tan recente, en vigor dende hai menos de medio século, xa que hoxe en día son moitas as aplicacións que atopa a xeometría fractal. Úsanse técnicas fractais en computación na compresión de datos e imaxes -a curva de Hilbert ten utilidade práctica nun proceso denominado dithering– e serven tamén para elaborar modelos matemáticos de multitude de formas naturais, dende os copos de neve até as redes fluviais, pasando polos nosos vasos sanguíneos, as liñas costeiras ou o movemento browniano aleatorio que seguen as partículas colocadas nun medio fluído.

Unha das utilidades máis sorprendentes dos fractais é ben coñecida por todo o mundo, pero seguramente insospeitada: o cinema. Loren Carpenter (n. 1947) é un diseñador de gráficos por computadora que creou o algoritmo de representación de Reyes, que emprega técnicas xeométricas e se ten usado para procesar imaxes complexas nas famosas películas de Pixar. Porén, aínda que dentro do mundo cinematográfico as películas de animación é onde menos estrañeza ha causar o uso das matemáticas, non é o único campo de aplicación que estas atopan.

E é que os fractais úsanse, en xeral, para crear representacións realistas de paisaxes que, simplemente, non existen. A primeira vez que o gran público puido ver unha escena así creada foi, grazas ao traballo de Carpenter, na película Star Trek II: The Wrath of Khan (1982), na cal as vistas que se amosan do planeta Genesis³ foron xeradas por fractais.

A idea detrás do deseño, moi básica, consiste en debuxar as paisaxes mediante triangulacións⁴. Para iso, pártese dunha rede de triángulos dotada de certa perspectiva tridimensional que se asemelle un chisco a, por exemplo, unha montaña (figura 2). Para acrecentar o parecido, reitérase a subdivisión de cada triángulo en catro novos triángulos construídos pola unión dos seus puntos medios. Así, en cada iteración do proceso o número total de triángulos cuadruplícase.

Partindo dunha rede inicial básica composta por 100 triángulos, na sétima iteración xa se supera o millón (para ser exactos, serían 1 638 400 triángulos). Se ao principio a semellanza cunha montaña era escasa, con tal cantidade de triángulos as formas xeométricas resultan indiscernibles e o resultado obtido dá o pego perfectamente unha vez que se dota á imaxe de cor, brillo e luz. Así que xa sabe, na próxima ocasión na que asista a unha proxección cinematográfica pode cuestionarse se algunha das escenas que presenciu se debe, en realidade, ás matemáticas.

Algunhas referencias:

• Argote, José Ignacio. “Peano”. Recuperado o 27/08/2023 desta ligazón.

• Doolan, Daniel C. “Examples of Graphics, Animation and Fractals in Movies”. Recuperado o 27/08/2023 desta ligazón.

• Mandelbrot, Benoît (2009). La geometría fractal de la naturaleza. Círculo de Lectores, Barcelona.

• Mandelbrot, Benoît (2000). Los objetos fractales. Tusquets Editores, Barcelona.

• Sorando Muzás, José María (2020). Matemáticas de Cine. Guadalmazán, Córdoba.