Napoleón e as matemáticas

Habitualmente relacionamos a Napoleón Bonaparte (1769 – 1821, figura 1) cos manuais de Historia, o cal ten todo o sentido do mundo porque se trata dun personaxe histórico de gran relevancia. Como militar e estadista, creo que a súa incidencia no devir dos asuntos europeos do século XIX é innegable. Pero Napoleón e as matemáticas tamén atopan unha vinculación. Son incuestionables os seus éxitos como estratega militar, e en todo caso sería discutible se os seus triunfos poden estar motivados en parte polos seus coñecementos matemáticos, xa que parece ser que entre as súas virtudes estaba o perfecto uso da artillaría e a xenial colocación dos canóns para realizar bombardeos.

Porque si, a diferenza da gran maioría dos políticos e gobernantes importancia, Napoleón tiña unha formación matemática bastante sólida. Xa na escola destacaba especialmente nas materias de Matemáticas e Xeografía, nas que conseguía excelentes cualificacións, e posterioremente acabou seguindo estudos superiores de artillaría na École Royale Militaire de París.

Napoleón naceu no ano 1769 e foi admitido na escola militar no 1784. Durante o tempo no cal era cadete alí, o matemático Pierre-Simon Laplace (1749 – 1827) era examinador de matemáticas en varias academias militares, entre elas a de artillaría de París. Cando falamos de Laplace facémolo dun matemático do primeiro nivel, un dos máis importantes da súa época, un que gañou por méritos propios un lugar destacado na historia das ciencias. Así, ademais do seu gusto pola materia, Napoleón podía alardear de ter sido discípulo de tan magno persoeiro.

En 1798, tras unha exitosa campaña en Italia e xa como xeneral do exército francés, Napoleón iniciou unha expedición militar co obxectivo de colonizar Exipto. Un dos aspectos máis sorprendentes da mesma foi que se rodeou dun bo número de especialistas científicos de diversas ramas, entre os cales se atopaban matemáticos do talle de Gaspard Monge (1746 – 1818) ou Jean-Baptiste Joseph Fourier (1768 – 1830).

Napoleón non só coñecía e situou cerca de si a varios matemáticos relevantes, senón que lles tiña moita confianza, até o punto de botar man deles para distintos cargos políticos. No 1799 nomeou a Laplace como ministro do Interior, aínda que só exerceu como tal durante seis semanas. Máis tarde, no ano 1805 Napoleón conferiríalle a Lexión de honra, a máis importante distinción francesa, e no 1806 concederíalle o título de conde do Imperio.

Tamén Monge gozou da confianza de Napoleón, tras coñecérense durante a campaña italiana. Acompañaría ao xeneral Bonaparte a Exipto coma un dos seus confidentes, e alí convertiríase no primeiro presidente do Instituto de Exipto. Xa de volta en Francia, e grazas a Napoleón, sería nomeado senador, conde e director da École Polytechnique.

Outro dos matemáticos que colaboraron con Napoleón foi Fourier, que o acompañou como asesor científico a Exipto onde o nomearía secretario do Instituto de Exipto. Os cargos de confianza continuarían en Francia, onde Napoleón o designou prefecto de Isère. A lista de matemáticos que podemos relacionar con Napoleón non acaba aquí, aínda que os tres xa citados foron os máis íntimos. Por citar un último caso, a Joseph-Louis de Lagrange -o director da tese doutoral de Fourier- concedeulle a Gran Cruz da Orde Imperial da Reunión dous días antes de que falecese.

Como vemos, Napoleón Bonaparte non era para nada alleo ao mundo das matemáticas como materia e dos matemáticos como profesionais. É sabido que unha das maiores honras que un matemático pode atopar é que un teorema se bautice co seu nome. Pois ben, no campo da xeometría atopamos un resultado que no 1826 se publicou baixo o nome de Teorema de Napoleón, afondando aínda máis se cabe a relación do antigo emperador francés coas matemáticas. Velaquí o porqué do título desta entrada: Napoleón e as matemáticas.

O seu enunciado pode ser algo así: se se constrúen tres triángulos equiláteros a partir dos lados dun triángulo calquera, entón os centros dos triánguos equiláteros forman tamén un triángulo equilátero (figura 2).

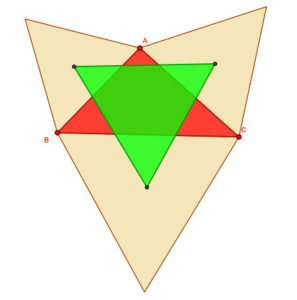
Só fai falla recordar que un triángulo equilátero é aquel que ten os seus tres lados iguais (na xeometría euclidiana tradicional, os triángulos equiláteros tamén son equiangulares e por tanto os seus ángulos internos son iguais). É, por tanto, unha proposición moi doada de entender porque todos os conceptos que emprega estúdanse hoxe en día no ensino obrigatorio (e incluso xa antes dos últimos cursos).¹

Porén, aínda que este teorema foi en ocasións atribuído ao propio Napoleón, parece pouco probable que fose demostrado por el. De feito, como xa se dixo a súa demostración non foi publicada até 1826, en The Ladies’ Diary, catro anos despois da morte de Napoleón. Foi William Rutherford quen propuxo o problema no número 122 da revista, e posteriormente apareceron dúas solucións (figura 3), unha dada por Mr. Tho. Burn e John Walker, a outra remitida por Mr. Mason.

Non obstante, o máis probable é que a primeira demostración deste teorema se deba a Lorenzo Mascheroni (1750 – 1800), matemático que coñeceu a Napoleón en 1796 durante a invasión francesa do norte de Italia. Mascheroni, gran admirador de Napoleón e sabedor da afición deste polas matemáticas, dedicoulle o seu libro Geometría del Compasso de 1797 e, con gran seguridade, honrouno bautizando co seu nome este teorema relativo a triángulos. Sexa como sexa, o nome de Napoleón vai quedar vencellado coas matemáticas para sempre. Non será unha relación moi forte, pero é suficiente como para falarmos un chisquiño sobre Napoleón e as matemáticas.

Algunhas referencias:

• Diestro Tejeda, Montserrat (2017). Geometría del triángulo. Teorema de Napoleón. Revista Suma n.º 84, pp 99-111.

• Durán, Antonio J. (2015). El universo sobre nosotros. Crítica, Barcelona.

1 Vostede pode experimentar co problema, de forma dinámica, premendo aquí.