Nas matemáticas gozamos cos xogos de azar. Non tanto buscando un beneficio económico nin motivados por unha competitividade que nos leve a buscar incansablemente a vitoria, senón máis ben polo reto intelectual que supón a súa análise. Trátase de estudar aspectos tales coma se se trata dun xogo xusto ou se a medio prazo hai unha perda/ganancia esperada. Ou tamén se algún dos xogadores mantén unha posición gañadora, é dicir, se un dos contendentes pode gañar todas as partidas sen importar a estratexia que siga o seu rival.
Neste apartado imos analizar un xogo de dados bastante sinxelo. Para dous xogadores, vostede e mais eu. Comeza vostede elixindo un dado e a continuación elixo eu outro. Lanzamos os dados elixidos e gaña a partida aquel que obteña unha maior puntuación na cara do dado que quede cara arriba. O típico, vamos. Ben, o típico no tocante ás regras do xogo, pero non tanto no que respecta aos dados que lle vou ofrecer, que son os da figura 1.
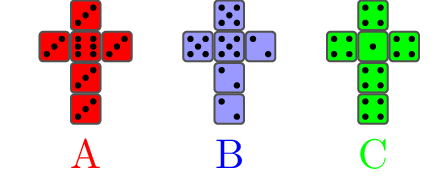
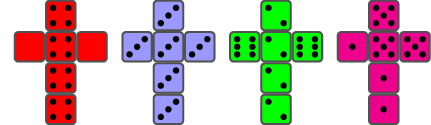
Como ben pode observar, amósollos “desmontados” para que se vexan as seis caras, pero basicamente trátase de dados cúbicos tradicionais nos que o único diferente é o valor que aparece nas caras. O dado A (vermello) ten 1 cara con 6 puntos e 5 caras con 3 puntos, o dado B (azul) ten 3 caras con 5 puntos e 3 caras con 2 puntos e o dado C (verde) ten 1 cara con 1 punto e 5 caras con 4 puntos.
Repare ben neles e nas súas caras, porque lembre que elixe vostede primeiro. Con que dado quedaría? Hai algún que sexa preferible ao outros? Quen leva vantaxe, vostede que elixe primeiro, ou eu que o fago despois pero coñecendo xa cal leva vostede? Ningún dos dous, quizais? Aí é onde reside un grande interese para os matemáticos, en analizar o xogo e ser quen de responder a estas preguntas.
Elixiu xa? Como eu non podo estar aí con vostede e non sei o que escolleu, vou estudar os tres posibles casos. Para cada un representarei os datos nunha táboa que recolla todas as posibles combinacións dos dous dados, a partir das cales tirarei a probabilidade de triunfo para cada un de nós. En todas elas porei na primeira columna, en vertical, os puntos do dado que colleu vostede e na primeira fila, en horizontal, os do dado que elixa eu.
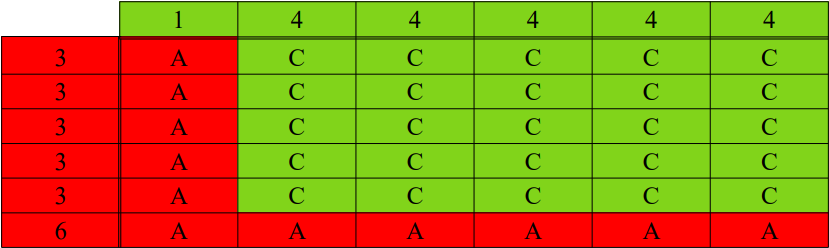
Se vostede colle o dado A (vermello), eu automaticamente tomo o dado C (verde), e as distintas posibilidades están enumeradas na táboa 1. Como se pode ver, teño todas as de gañar porque a probabilidade é de 25/36 ao meu favor; só 11 das 36 combinacións lle permitirían gañar a vostede, aquelas nas que eu saco o 1 e aquelas nas que vostede saca o 6.
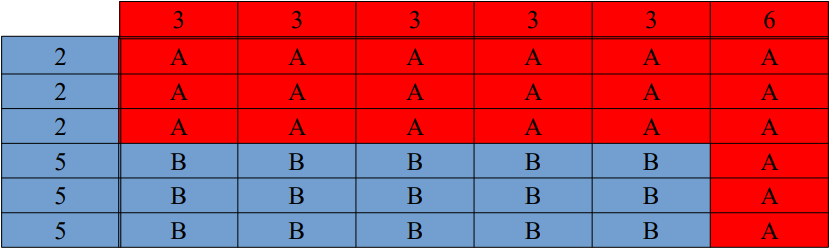
Se por contra vostede optase por coller o dado B (azul), eu veríame na obriga de elixir o dado A (vermello), o cal se recolle na táboa 2. Como pode comprobar facilmente, aínda que a unha partida pode ocorrer calquera cousa se prolongásemos o xogo as probabilidades estarían do meu lado. Isto é porque en promedio gañarei 21 de cada 36 veces, mentres que vostede só o fará 15 de cada 36. A diferenza é menor que no caso anterior, pero de cara á vitoria sigo sendo o favorito.
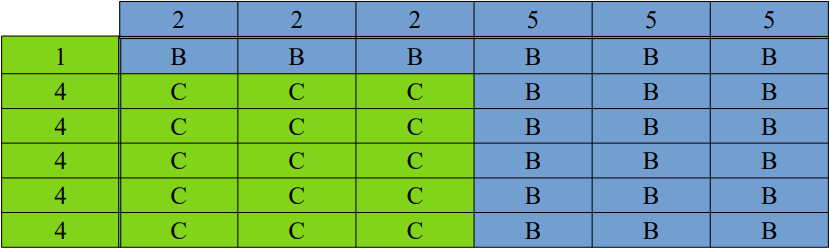
Por último, vostede pode optar polo dado C (verde) e en tal caso eu escollerei o dado B (azul). Fíxese na táboa 3 e verá que con esta opción a probabilidade de que triunfe eu é de 21/36 e a de que gañe vostede é de 15/36, ao igual ca antes.
Dáse conta, non si? Resulta indiferente cal sexa a súa escolla, opte por un dado ou por outro eu sempre podo elixir un dos que queda de tal xeito que terei unha notable vantaxe cando nos poñamos a xogar. Unha vantaxe que me outorga o cálculo de probabilidades, e que se resume esquematicamente na figura 2. Aos dados que cumpren isto dámoslle o nome de dados non transitivos.
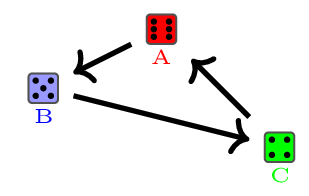
Eu non sei se cando lle expliquei as regras do xogo vostede contaba con que agromase tal circunstancia. Pero algo seguro que sospeitaba, se non, que interese podería ter eu en amosar neste espazo un xogo así? En matemáticas, cando sucede o que aquí nos pasou cos dados dicimos que unha relación carece da propiedade transitiva. No mundo real estamos pouco acostumados á ausencia de transitividade. Se Bea é máis alta que Alba e Carme é máis alta que Bea, inmediatamente aseguramos sen temor a equivocarnos que Carme é máis alta que Alba. “Ser máis alto que” é unha relación que si cumpre a propiedade transitiva, pero non é necesariamente certo en todos os sistemas, como ben acabamos de comprobar cos dados. Porén, na mesma liña ca este dos dados, existe outro xogo non transitivo máis simple e moi coñecido por estes lares: o que se adoita chamar ‘pedra, papel, tesoira’. Recoñece as similitudes entre ambos?
Os dados que eu lle ofrecín non son os únicos que presentan esta particularidade. Tamén sucede, por exemplo, cos que teñen puntuacións 2, 2, 6, 6, 7, 7 para un dos dados, 1, 1, 5, 5, 9, 9 para outro e 3, 3, 4, 4, 8, 8 para o último, co engadido de que neste trío as probabilidades que se obteñen nos tres posibles casos son as mesmas (no noso exemplo, dúas eran iguais e outra diferente). E non estamos limitados só a tres dados, pois con catro dados Bradley Efron (n. 1938) inventou o xogo que se ve na figura 3, no cal cada dado se ve batido polo anterior (e o primeiro polo último) cunha probabilidade de 2/3.
Podemos atopar moitas e variadas versións, con 5 dados, ou con 7, ou unha moi curiosa proposta por Shirley Quimby (1893 – 1986) con 4 dados que empregan todos os números naturais do 1 ao 24 unha única vez cada un. E non só hai que restrinxirse aos dados cúbicos, xa que existen dados non transitivos con outras formas. Dodecaedros, por exemplo, con 12 caras cada un dos 3 dados. Ou tetraedros, xogo que pode atopar vostede no Museo de Matemáticas de Cataluña, visita que lle recomendo se algún día anda por Cornellà de Llobregat.
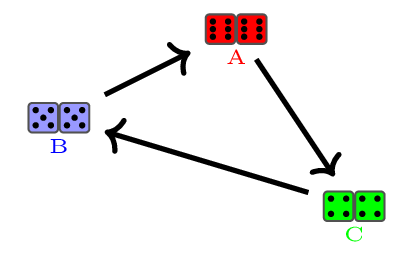
Para rematar con isto dos dados non transitivos, voulle ofrecer que botemos unha nova partida ao xogo inicial. A revancha. E vou elixir dado eu o primeiro. Agora que vostede xa coñece o truco, sabe cal ten que elixir para que a probabilidade lle axude a vencerme. Pero dando unha volta de torca ao asunto, agora imos empregar dous dados no canto de un. É dicir, que eu elixo que tipo de dado quero, pero lanzo dous dados iguais, e vostede coa súa elección tamén. Non me vou estender coas explicacións, déixolle que as debulle vostede, pero o resultado é sorprendente: o esquema da figura 2 invértese! O verde xa non lle gaña ao vermello, senón que con dous dados é o vermello o que lle gaña ao verde, e o mesmo pasa cos outros dous casos (figura 4). Desconcertante, non si?
Algunhas referencias:
- Gaussianos. “Esos curiosos dados”. Recuperado o 20/08/2023 desta ligazón.
- Grima, Clara. “Tengo unos dados (no transitivos) y no dudaré en ganarte”. Recuperado o 20/08/2023 desta ligazón.
- Grime, James. “Non-transitive Dice”. Recuperado o 20/08/2023 desta ligazón.
- Museo de Matemáticas de Cataluña. “Daus intrasitius”. Recuperado o 20/08/2023 desta ligazón.
- Parker, Matt (2020). Pifias matemáticas: equivocarse nunca ha sido tan divertido. Editorial Planeta, Barcelona.
- Tanton, James S. (2019) ¡Resuélvelo! Retos lúdicos para curiosos de las matemáticas. Colección Estímulos Matemáticos, Ediciones SM, Madrid.